Question

При паралельному перенесенні трикутник АВС перейшов у трикутник А'В'С'. Знайдіть кути трикутника АВС, якщо трикутник А'В'С' є рівнобедреним з основою А'В' і угол В' = 40​

Answer 1

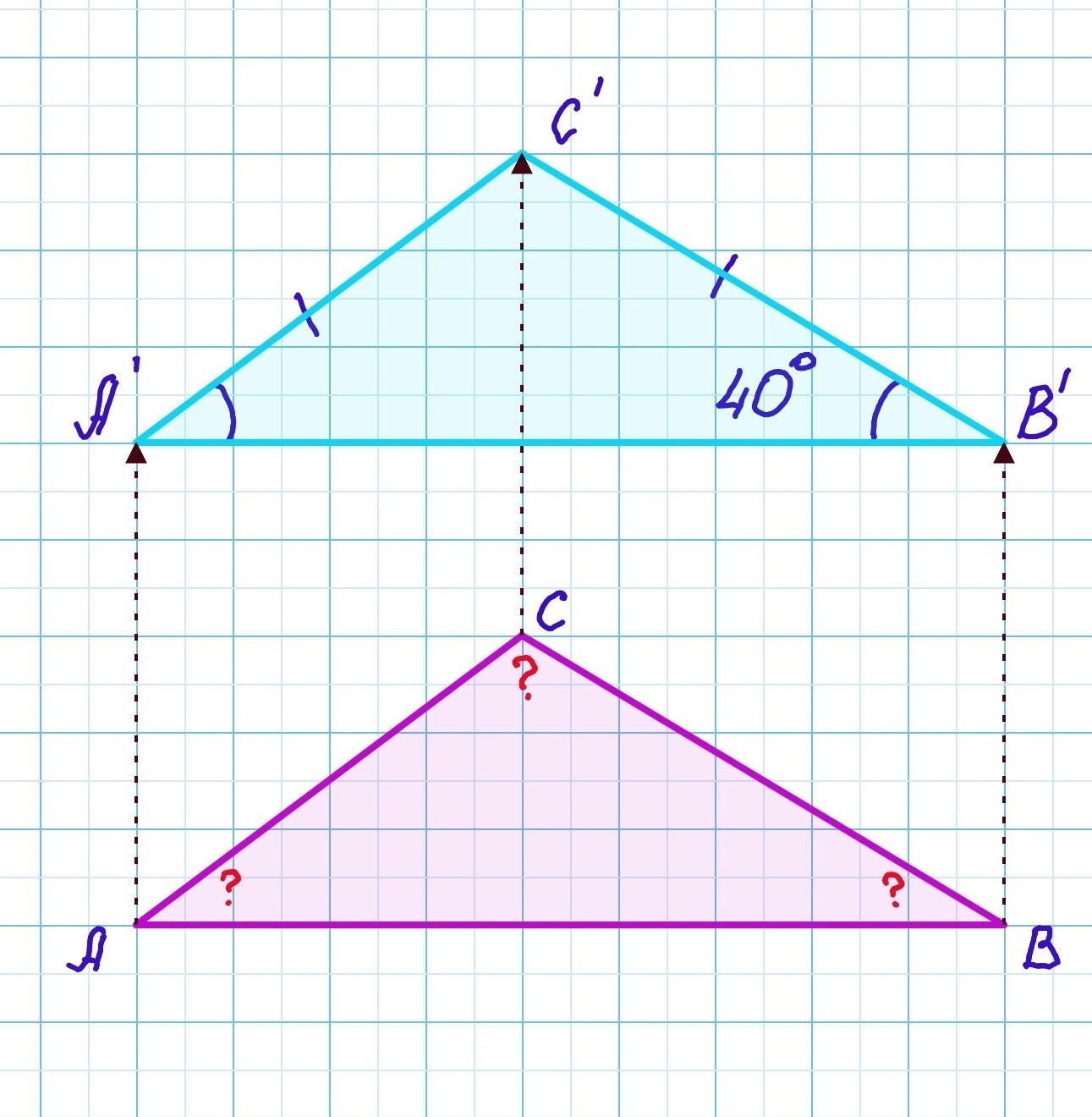
При паралельному перенесенні трикутник АВС перейшов у трикутник А'В'С'. Знайдіть кути трикутника АВС, якщо трикутник А'В'С' є рівнобедреним з основою А'В' і угол В' = 40°

Ответ:

∠А=40°, ∠В=40°, ∠С=100°

Объяснение:

• Паралельним перенесенням на вектор $\overrightarrow{p}$ називають таке перетворення, при якому кожній точці А відповідає така точка А', що $\overline{AA'}=\overrightarrow{p}$
• Паралельне перенесення є переміщенням.
• Переміщення - це перетворення однієї фігури в іншу, коли воно зберігає відстань між точками, тобто переводить будь-які дві точки А і В першої фігури в точки А' і В' другої так, що АВ = А'В'.
• Під час переміщення кут переходить у рівний кут.

РІШЕННЯ:

1) Знайдемо кути △А'В'С'.

За умовою він рівнобедрений. А'В' - основа.

В рівнобедреному трикутнику кути при основі рівні.

Сума кутів трикутника дорівнює 180°, тому:

∠А'=∠В'=40°.

∠С'=180°-∠А'-∠В'=180°-40°-40°=100°

2) Початкова фігура та фігура, отримана після паралельного перенесення, рівні.

Тобто за властивостю переміщення маємо:

∠А'=∠А=40°

∠С'=∠С=100°

∠В'=∠В=40°

#SPJ1