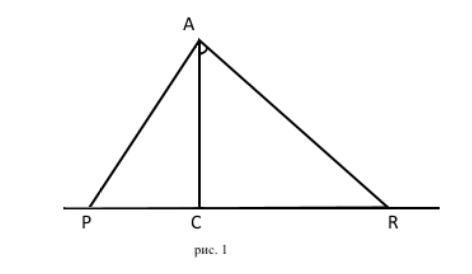
(СРОЧНО!!! ДАЮ 100 БАЛЛОВ!!!) На фото (рис. 1), AC перпендикулярний PC. Похилі, які проведено з точки A до прямої PC, перпендикулярні. Відстань між основами цих похилих 12 см, а відношення проекцій похилих 1 : 3. Знайти відстань від точки A до прямої PC.
Ответы
AC перпендикулярний PC. Похилі, які проведено з точки A до прямої PC, перпендикулярні. Відстань між основами цих похилих 12 см, а відношення проекцій похилих 1 : 3. Знайти відстань від точки A до прямої PC.
Ответ:
Відстань від точки A до прямої PC дорівнює 3√3 см
Объяснение:
АС - перпендікуляр, проведений з точки А до прямої РС. АС⟂РС. Точка С - основа перпендикуляра АН.
АР і AR - похили, проведені з точки А до прямої РС. Точки Р і R - основи похилої.
- Похила- будь-який відрізок, проведений із точки на пряму, відмінний від перпендикуляра.
РС і CR - проекції похилих AP і AR.
- Проекція похилої на пряму - відрізок, що сполучає основу перпендикуляра і основу похилої до прямої.
Відстань між основами похилих: PR=12 см.
Відношення проекцій похилих: PC: CR = 1 : 3.
Хай PC =х, тоді CR=3х. Так як PR=12 см, то:
PC+CR=PR
x+3x=12
4x=12
x=3
PC =х=3см, CR=3х=3×3=9см.
- Відстань від точки до прямої дорівнює довжині перпендикуляра, опущенного з точки на пряму.
АС⟂РС. Знайдемо АС.
За умовою похилі, які проведено з точки A до прямої PC, перпендикулярні.
Розглянемо прямокутний трикутник PAR(∠А=90°).
- Перпендикуляр, опущений з вершини прямого кута на гіпотенузу, дорівнює середньому геометричному проекції катетів на гіпотенузу.
AC²=PC•CR
AC²=3×9=27
AC=√27=3√3 см
#SPJ1
