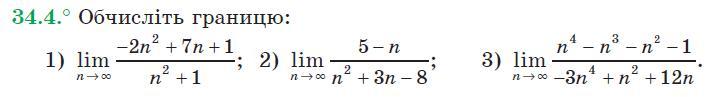Ответы
Ответ дал:
0
Ответ:
Объяснение:
Ответ дал:
0
Т.к. х→∞, то задания решаются устно,
1)-2, т.к. максимальные степени вторые в числителе и знаменателе имеют одинаковые вторые степени. просто делим коэффициенты при них -2/1=-2
2)0, т.к. максимальная степень числителя меньше максимальной степени знаменателя.
3)-1/3 аналогично 1) т.к. показатели максимальных степеней одинаковы, т.е. 4 степень и в числителе, и в знаменателе, делим их коэффициенты. 1/(-3)=-1/3
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад