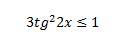Ответы
Ответ дал:
0
Решение.
Применяем метод интервалов .
знаки: + + + + + [-1/√3] - - - [1/√3] + + + + +
Ответ:
Вас заинтересует
2 года назад
2 года назад
8 лет назад