Question

СРОЧНО 20 БАЛЛОВ
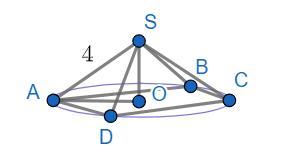
задан конус в который вписана правильная четырехугольная пирамида SABCD.Образующая конуса SA равна 4 и наклонена к плоскости основания под углом 30 градусов. Найдите объем конуса.

Answer 1

Ответ:

Объем конуса = 8π (единицы измерения в условиях задачи не даны)

Объяснение:

Сделаем чертеж. Пусть О- основание высоты конуса и пирамиды, центр окружности в основании конуса (так как пирамида правильная).

В прямоугольном треугольнике SAO длина гипотенузы SA равна 4, значит катет, лежащий напротив угла SAO в 30 градусов будет равен половине гипотенузы, значит SO=4/2=2.

AO найдем по теореме Пифагора:

AO²=SA²-SO²=16-4=12

Площадь основания конуса равна площади окружности с радиусом AO, значит равна π×AO²=12π

Объем конуса равен 1/3 произведения площади основания на высоту SO = 1/3 * 12π * 2=8π

#SPJ1