помогите пожалуйста
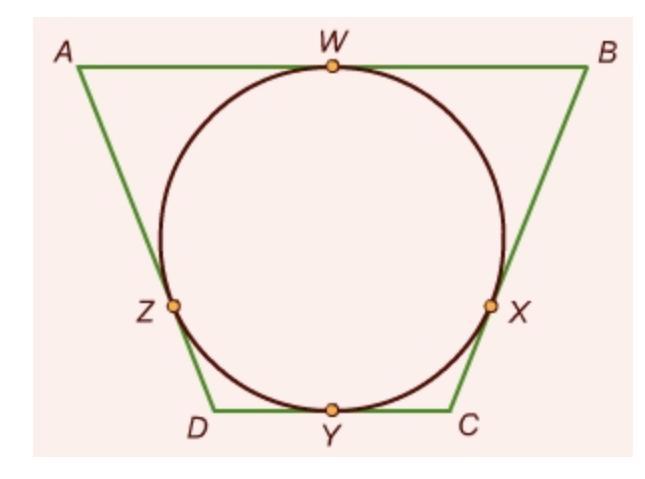
Дан четырехугольник ABCD, в который вписана окружность: |BX| = 13, |CD| = 12, |AW| = |WB|, |DZ | = |CX|. Чему равен периметр четырехугольника ABCD?
СРОЧНО
Приложения:
lizaillyashenko:
Как часы ;-)
Ответы
Ответ дал:
1
Ответ:
100
Пошаговое объяснение:
13+13+13+13+12+12+12+12=100
это точно?
Как часы ;-)
ты уверена на 100%?
решения нет
Согласно какой-то теореме (название не помню) AC=AW, CD=CY, CY=CX, и BW=BX. Согласно условию AW=WB, DZ=CX. Цифры в условии даны. Складываем – получаем ответ. Прости, я плохо объясняю...
в условие вчитайтесь
Ответ дал:
0
т.к. окружность вписана в четырехугольник, то по свойству отрезков, проведенных из одной точки к одной окружности следуют такие равенства
АZ=AW
BW=BX=13
DZ=DY
CX=CY
CD=12, если СУ=х, то DY=12-х
АZ=AW=BW=13
BW=BX=13
DZ=DY=12-х
CX=CY=х
периметр четырехугольника ABCD равен сумме его сторон АD+AB+CB+DC . состоящих из отрезков,
Р= АD+AB+CB+DC=(АZ+DZ)+(AW+BW)+(CX+BX)+(CY+DY)=
13+12-x+13+13+x+13+x+12-x=4*13+2*12=52+24=76
Ответ 76
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад