Question

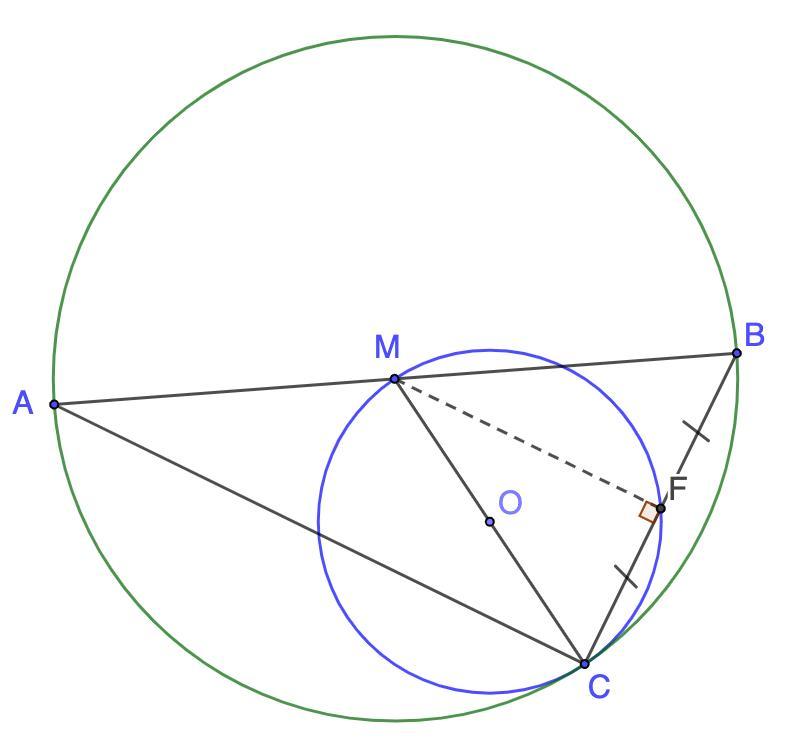
Задан треугольник ABC, AB = 8. Из вершины C проведена медиана CM. На медиане CM как на диаметре построена окружность, которая пересекает сторону BC в точке F так, что F – середина BC. Найдите радиус окружности, описанной около треугольника ABC.

Answer 1

Ответ:

Радиус окружности, описанной около треугольника ABC равен 4 ед.

Объяснение:

Требуется найти радиус окружности, описанной около треугольника ABC.

Дано: ΔАВС;

СМ - медиана;

Окр.О; СМ - диаметр;

Окр.О ∩ ВС = F; BF = FC;

AB = 8;

Около ΔАВС описана окружность.

Найти: R описанной окружности около ΔАВС.

Решение:

Соединим точки F и М.

1. Рассмотрим ΔСМВ.

BF = FC (условие)

⇒ МF - медиана;

• Вписанный угол, опирающийся на диаметр, равен 90°.

⇒ ∠MFC = 90°.

⇒ МF - высота.

• Если в треугольнике медиана является высотой, то этот треугольник равнобедренный.

⇒ СМ = МВ.

2. Рассмотрим ΔАВС.

АМ = МВ (СМ - медиана)

СМ = МВ (п.1)

⇒ СМ = МВ = АМ

• Если в треугольнике медиана равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.

⇒ ∠С - прямой.

• Если вписанный угол прямой, то он опирается на диаметр.

⇒ АВ - диаметр описанной окружности.

• Радиус равен половине диаметра.

⇒ R = АВ : 2 = 8 : 2 = 4 (ед.)

Радиус окружности, описанной около треугольника ABC равен 4 ед.

#SPJ1