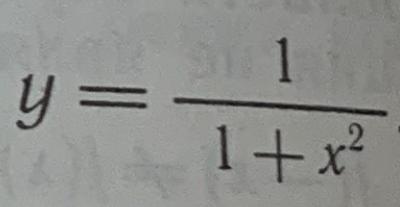Question

Помогите исследовать функцию и построить график

Answer 1

$y=\frac{1}{1+x^2}$

Начнём с того, что функция определена на всей числовой прямой и чётная.

Значит, можем построить график при x >= 0 и отразить его относительно оси Y.

Найдём производную как производную сложной функции:

$y' = -\frac{1}{(1+x^2)^2}*2x = \frac{-2x}{(1+x^2)^2}$

При x >= 0 y' <= 0. Значит при x >= 0 функция убывает. Критических точек нет, стационарная точка - x = 0.

Так как справа от x = 0 функция убывает, то слева - возрастает (так как функция чётная). Значит, x = 0 - точка максимума.

Заметим также, что у графика есть горизонтальная асимптота y = 0:

$\lim_{x \to \infty} (\frac{1}{1+x^2}) = 0$

Таким образом, функция ограничена сверху единицей (при x = 0), снизу - нулём.

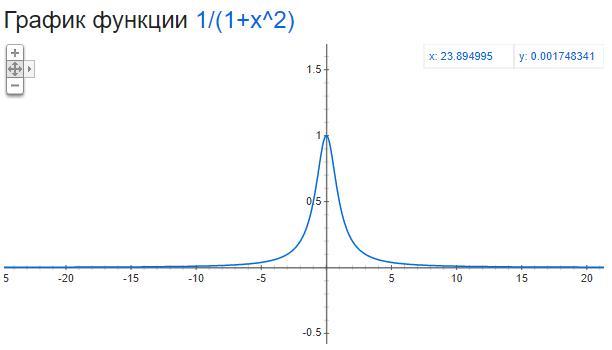
Осталось вычислить значение в некоторых положительных точках и провести линию графика, а затем отразить её относительно оси Y. График - на рисунке.