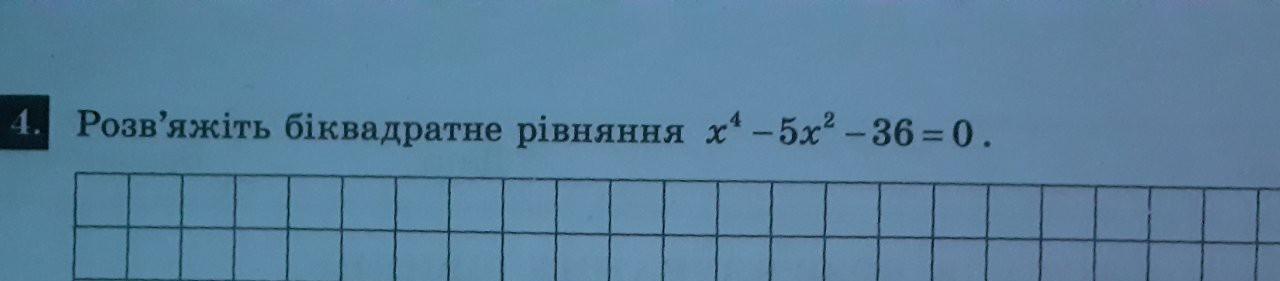Ответы
Ответ дал:
2
Ответ:
± 3
Объяснение:
Ответ дал:
0
Відповідь:
Нехай x^2=t, тоді:
t^2-5t-36=0
D=b^2-4ac= (-5)^2 -4(-36) =4*36+25=144+25=169=13^2
t1 = 5+13/2=9; t2= 5-13/2=-4.
x^2=-4 - не належить R
x^2=9
Відповідь: x1 = -3, x2=3
Пояснення:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад