Ответы
Ответ дал:
0
Ответ:
Объяснение:
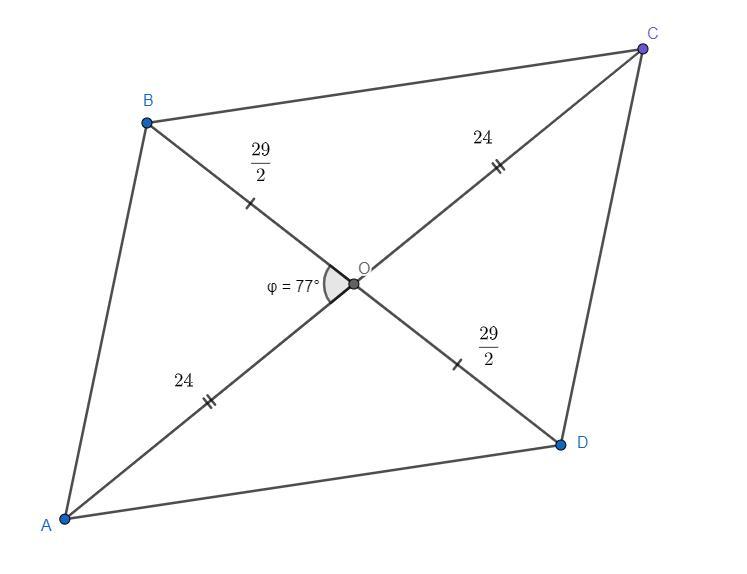
- паралелограмм, тогда диагонали
и
делятся точкой пересечения
пополам. Тогда длины отрезков
Запишем теорему косинусов для треугольника
Запишем теорему пифагора для треугольника
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад