Ответы
Ответ дал:
0
Ответ:
Объяснение:
Нам дана производная
Найдем ее нули
Найдем знаки производной. Где знак +, там функция возрастает - см. рисунок
Запишем ответ:
Приложения:
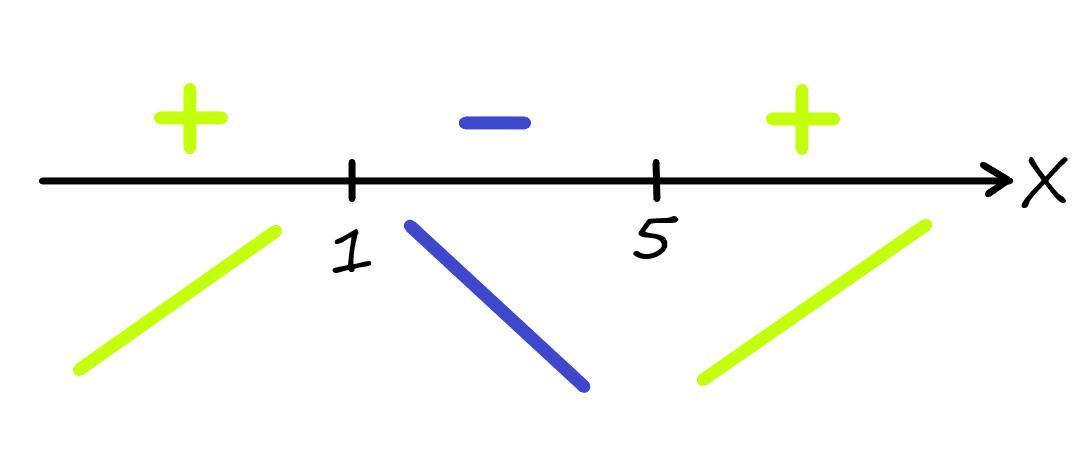
Ответ дал:
1
Ответ:
( -∞; 1]∪[ 5; +∞)
Объяснение:
f'(x)=(x-1) (x-5)
f'(x)=0 <-> (х-1)(х-5)=0
х^2-6х+5=0
[х1=1; х2=5;
( -∞; 1]∪[ 5; +∞)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад