Question

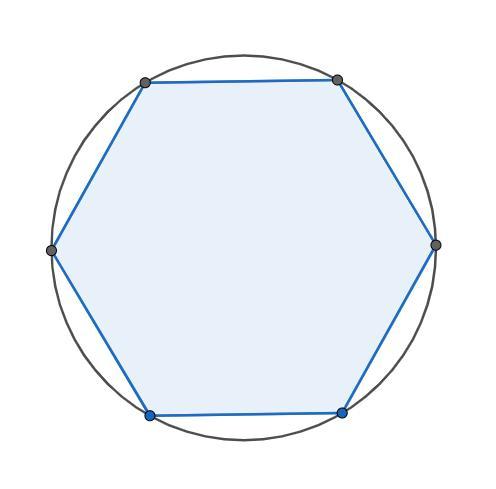
В круг вписан правильный шестиугольник. Найти вероятность того, что точка, наудачу брошенная в круг, не попадёт в правильный шестиугольник, вписанный в него.​

Answer 1

Ответ:

$\dfrac{2\pi-3\sqrt{3}}{2\pi}\approx 0.173$

Объяснение:

Вероятность того, что точка не попадет в шестиугольник равна 1 минус вероятность того, что точка попадет в шестиугольник (сумма вероятностей двух взаимоисключающих событие равна 1), т.е.

$P(A)+P(\bar A)=1$

Вероятность того, что точка попадет в шестиугольник равна отношению площадей круга и шестиугольника, т.е.

$P(\bar A)=\dfrac{S}{S_\circ}$

У шестиугольника сторона $a$ равна радиусу описаной окружности $R$, и его площадь равна

$S=\dfrac{3\sqrt{3}}{2}a^2=\dfrac{3\sqrt{3}}{2}R^2$

Площадь круга $S_\circ=\pi R^2$

Выразим их отношение

$P(\bar A)=\dfrac{S}{S_\circ}=\dfrac{\dfrac{3\sqrt{3}}{2}R^2}{\pi R^2}=\dfrac{3\sqrt{3}}{2\pi}$

Тогда искомая вероятность

$P(A)=1-P(\bar A)=1-\dfrac{3\sqrt{3}}{2\pi}=\dfrac{2\pi-3\sqrt{3}}{2\pi}\approx 0.173$

Answer 2

Ответ:

$1-\frac{3\sqrt{3}}{2\pi}$

Объяснение:

Площадь круга с радиусом R равна πR²

Площадь шестиугольника, вписанного в круг радиуса R равна $\frac{3\sqrt{3}}{2}R^2$

Событие А - точка, наудачу брошенная в круг, не попадёт в правильный шестиугольник, вписанный в него (т.е. попадет в поле, отмеченное на рисунке желтым цветом)

P=m/n - классическое определение вероятности, где n - число всех равновозможных элементарных исходов, m - число благоприятствующих событию исходов.

$n=\pi R^2\\\\m=\pi R^2-\frac{3\sqrt{3}}{2}R^2=\frac{(2\pi -3\sqrt{3})R^2}{2}$

$P(A)=\frac{\frac{(2\pi-3\sqrt{3})R^2}{2}}{\pi R^2}=\frac{(2\pi-3\sqrt{3})R^2}{2\pi R^2}=\frac{2\pi -3\sqrt{3}}{2\pi}=1-\frac{3\sqrt{3}}{2\pi}$