Помогите сделать интеграл, пожалуйста! 100 баллов даю. Глупые ответы не давать, блокирую за нарушение правил сразу!
Приложения:
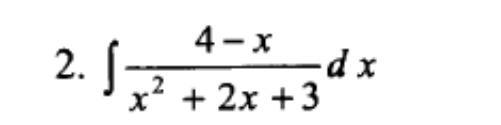
Ответы
Ответ дал:
1
В решении производится замена переменной x на t и u. Всё сводится к табличным интегралам для логарифма и арктангенса.
После всех этих преобразований можем приступить к расчётам.
ТвойНочнойКошмар:
Ого… спасибо огромное
корону ему дай
а, молодец
я бы задолбался писать все в редакторе формул
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад