Question

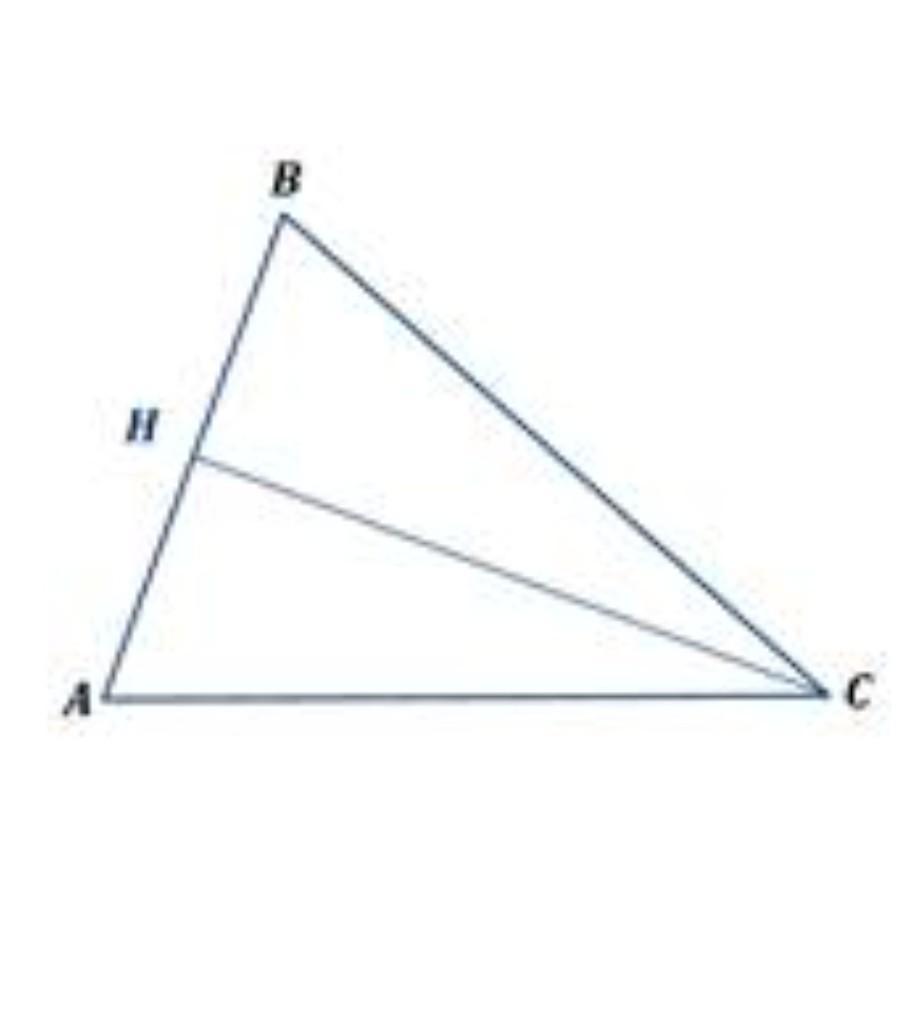
В треугольнике АВС, проведен серединный перпендикуляр СН к стороне АВ. Угол В равен 74°. Найдите угол АСН. ​

Answer 1

Ответ:

Угол АСН равен 16°.

Объяснение:

В треугольнике АВС, проведен серединный перпендикуляр СН к стороне АВ. Угол В равен 74°. Найдите угол АСН. ​

Дано: ΔАВС.

СН - серединный перпендикуляр;

∠В = 74°.

Найти: ∠АСН

Решение:

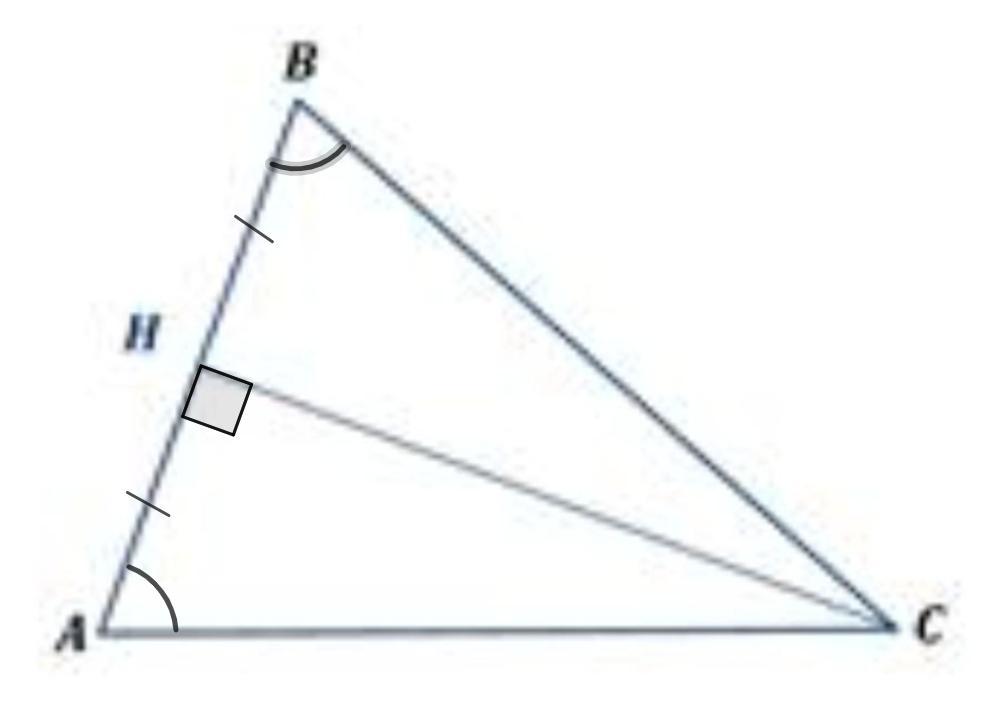
Рассмотрим ΔАВС.

СН - серединный перпендикуляр.

Серединный перпендикуляр — прямая, перпендикулярная данному отрезку и проходящая через его середину.

⇒ АН = НВ, то есть, СН - медиана;

СН ⊥ АВ, то есть, СН - высота.

• Если в треугольнике высота является медианой, то этот треугольник равнобедренный.

⇒ ΔАВС - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠А = ∠В = 74°

• Сумма углов треугольника равна 180°.

⇒ ∠С = 180° - (∠А + ∠В) = 180° - 148° = 32°

• В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой.

⇒ ∠ВСН = ∠АСН = ∠С : 2 = 32° : 2 = 16°

Угол АСН равен 16°.

#SPJ1