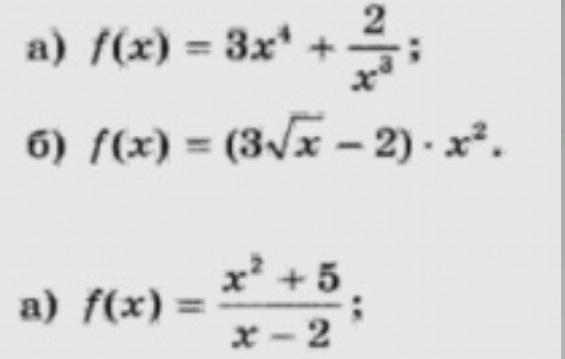Ответы
Ответ дал:
2
(u±v)'=u'±v'
(u*v)'=(u'v+uv')
(u/v)'=(u'v-uv')/v²
(√x)'=1/(2√x)(xⁿ)'=n*xⁿ⁻¹
(const)'=0
a) f'(x)=(3x⁴+2/x³)'=12x³-6/x⁴
b) f'(x)=(3/(2√x))*x²+2x*(3√x-2)=(3x²/(2√x))+2x*(3√x-2)
c) f'(x)=(2x*(x-2)-(x²+5))/(x-2)²=(2x²-4x-x²-5)/(x-2)²=(x²-4x-5)/(x-2)²
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад