Покрашенный кубс размером 4 x 4х4 см разрезали на кубики с размерами 1х1х1 см. Определи, сколько в составе куба кубиков, которые имеют: 1. три покрашенные грани - кубиков; 2. все грани непокрашенные грани – кубиков.

Ответы
Ответ:
1. Три покрашенные грани имеют 8 кубиков;
2. Все грани не покрашенные грани 8 кубиков.
Пошаговое объяснение:
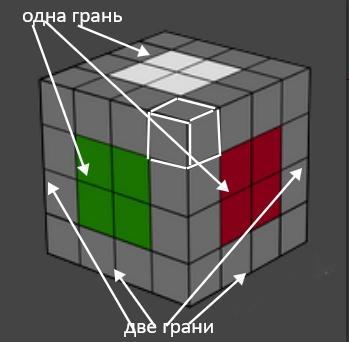
У куба 12 ребер, 8 углов и 6 граней (см. рисунок).
При распиливании куба с размером 4×4×4 получится всего
4·4·4:(1·1·1) = 64:1 = 64 кубика с размером 1×1×1.
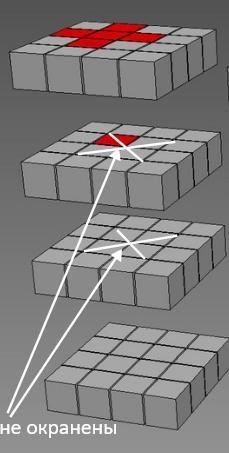
С трех сторон могут быть окрашены только кубики находившиеся по углам большого куба (белые кубики).
1 · 8 = 8.
С двух сторон могут быть окрашены кубики находившиеся на ребрах большого куба (зелёные кубики) за исключением угловых кубиков. Каждое ребро содержит два не угловых кубика.
2 · 12 = 24.
Найдем еще кубики, окрашенные с одной стороны (оранжевые кубики). Такие кубики были расположены на гранях большого куба и не принадлежали углам и ребрам. На каждой грани четыре таких кубика.
4 · 6 = 24.
Оставшиеся кубики не окрашены:
64 – 24 – 24 – 8 = 8.
#SPJ1
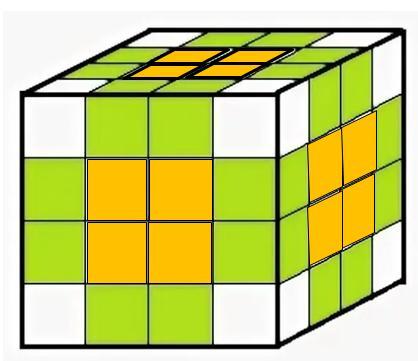
Ответ:
1) три окрашенных грани 8 кубиков
2) все грани непокрашенные грани 8 кубиков
Пошаговое объяснение:
У куба 12 ребер, 8 углов и 6 граней.
Всего кубиков 4 × 4 × 4 = 64
1. три покрашенные грани имеют только кубики, стоящие в углах большого куба.
Следовательно, три окрашенных грани имеют 8 кубиков.
2. все грани не окрашены.
Считаем
Мы уже выяснили, что с трех сторон покрашены 8 кубиков.
Посчитаем окрашенные с двух сторон.
Это кубики на ребрах.
Каждое ребро содержит по 2 кубика (это за минусом угловых)
2 × 12 = 24.
И кубики, окрашенные с одной стороны. Это по 4 кубика на грань (за минусом угловых и боковых)
4 × 6 = 24
Итого неокрашенных кубиков
64 - 24 - 24 - 8 = 8
Таким образом, не крашено 8 кубиков
#SPJ1