Question

Різниця відрізків, на які висота прямокутного трикутника поділяє
гіпотенузу, дорівнює 10 см. Знайдіть площу трикутника, якщо його висота, проведена до гіпотенузи, дорівнює 12 см.

Answer 1

Ответ:

Площадь треугольника равна 156 см ²

Объяснение:

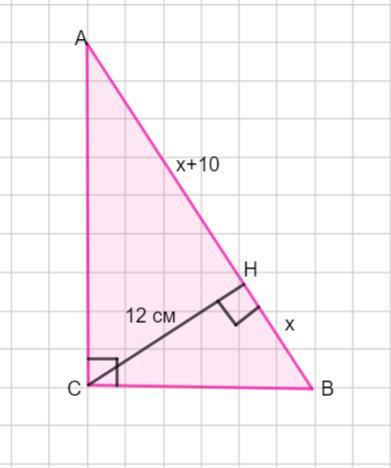
Пусть дан Δ АВС - прямоугольный. В треугольнике проведена высота СН =12 см. Высота делит гипотенузу на отрезки АН и ВН , причем АН на 10 см больше отрезка ВН.

Надо найти площадь треугольника.

Пусть ВН =х см, АН =(х+10) см. Так как высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое между отрезками, на которые гипотенуза делится основанием высоты, то составляем уравнение.

$CH=\sqrt{AH\cdot BH } ;\\CH^{2}= AH\cdot BH;\\(x+10)\cdot x=12^{2} ;\\x^{2} +10x=144;\\x^{2} +10x-144=0;\\D=10^{2} -4\cdot1\cdot(-144)=100+576=676=26^{2} ;\\\\x{_1}= \dfrac{-10-26}{2} =-\dfrac{36}{2} =-18;\\\\x{_2}= \dfrac{-10+26}{2} =\dfrac{16}{2} =8$

Условию задачи удовлетворяет положительное значение. Значит,

ВН =8 см, АН =8+10 =18 см.

Тогда гипотенуза АВ =ВН+АН=18 + 8 =26 см .

Найдем площадь треугольника, как полупроизведение гипотенузы на высоту, проведенную к ней.

$S = \dfrac{1}{2} \cdot AB \cdot CH;\\\\S =\dfrac{1}{2} \cdot 26\cdot 12 =13\cdot 12=156$

Тогда площадь треугольника равна 156 см ²

#SPJ1