Question

В равнобедренную трапецию вписана окружность. Найди радиус это окружности, если основания трапеции равны 15 см и 24 см.

Answer 1

Ответ:

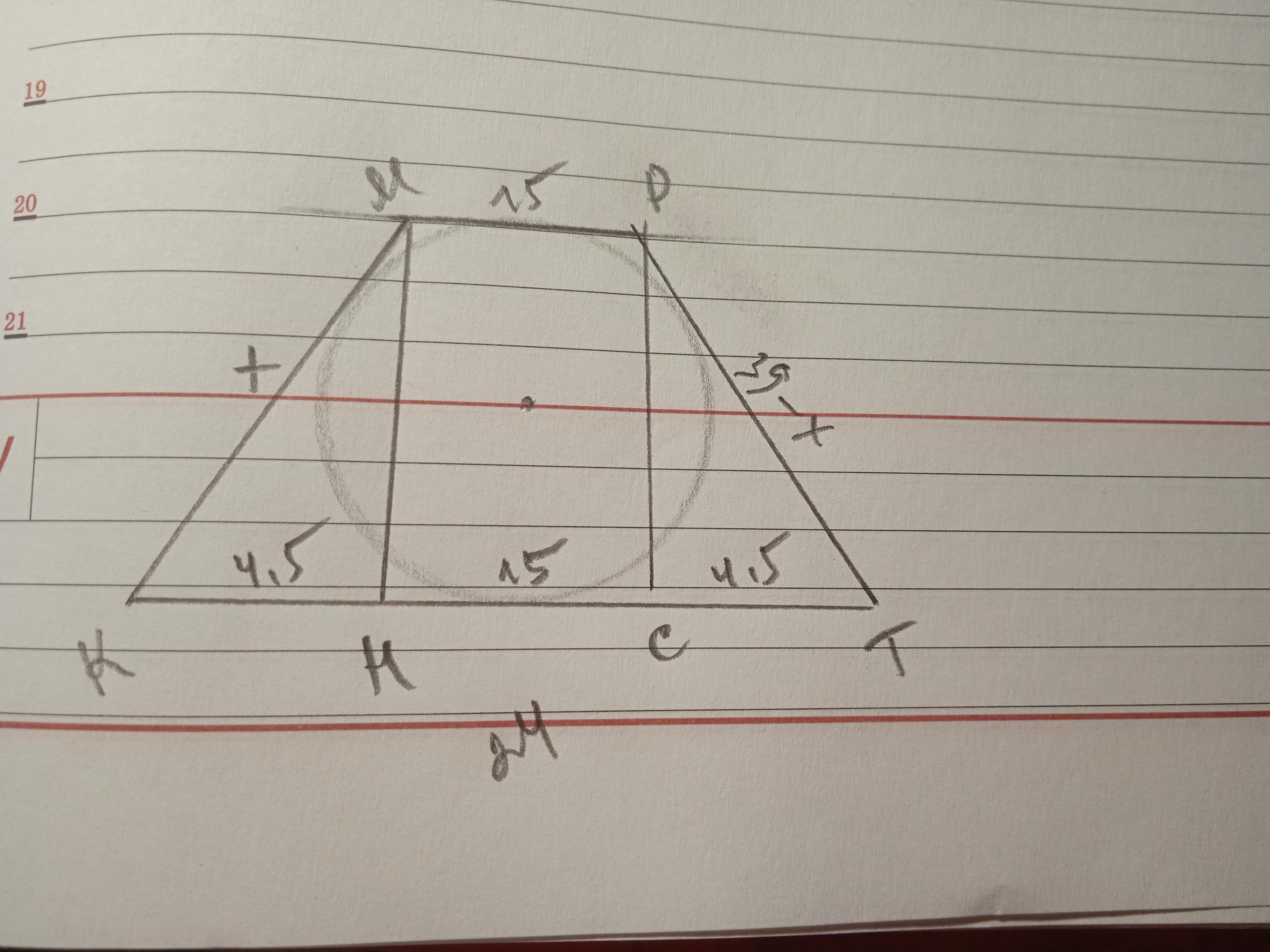
решение смотри на фотографии

Answer 2

Ответ:

3√10 см.

Объяснение:

Если в трапецию можно вписать окружность, то сумма оснований равна сумме боковых сторон.

Диаметр этой окружности равен высоте трапеции.

Дано: КМРТ - трапеция, КМ=РТ,  МР=15 см, КТ=24 см.   r - ?

15+24=39 (см) сумма оснований и сумма боковых сторон

Пусть КМ=х см, тогда РТ=39-х см.

Проведем высоты МН и РС. ΔКМН=ΔТРС по катету и гипотенузе.

КН=СТ=(24-15):2=4,5 см.

По теореме Пифагора МН=√(КМ²-КН²)  РС=√(РТ²-СТ²)

√(КМ²-КН²)=√(РТ²-СТ²)

√(х²-20,25)=√((39-х)²-20,25)

х²-20,25=1521-78х+х²-20,25

78х=1521;  х=19,5;  КМ=РТ=19,5 см.

МН=√(380,25-20,25)=√360=6√10 см.

r=1/2 МН=3√10 см.