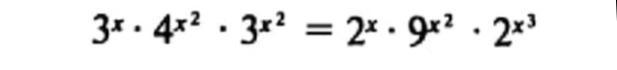Ответы
Ответ дал:
1
Ответ:
0; 1; ㏒₂3+1
Пошаговое объяснение:
перепишем уравнение с учетом того, что 4=2²; 9=3²
3ˣ*4ˣ²*3ˣ²=2ˣ*9ˣ²*2ˣ³
3ˣ²⁺ˣ*2²ˣ²=2ˣ⁺ˣ³*3²ˣ²
разделим обе части уравнения на 3²ˣ²*3²ˣ²
получим 3ˣ²⁺ˣ/3²ˣ²=2ˣ⁺ˣ³/2²ˣ²
3ˣ²⁺ˣ⁻²ˣ²=2ˣ⁺ˣ³⁻²ˣ²
3ˣ⁻ˣ²=2ˣ⁺ˣ³⁻²ˣ²
3ˣ⁽¹⁻ˣ⁾=2ˣ⁽¹⁺ˣ²⁻²ˣ⁾
3ˣ⁽¹⁻ˣ⁾=2ˣ⁽¹⁻ˣ⁾²
прологарифмируем обе части уравнения по основанию 2,А получим ㏒₂3ˣ⁽¹⁻ˣ⁾=㏒₂2ˣ⁽¹⁻ˣ⁾²
х*(х-1)㏒₂3=х*(х-1)²
х*(х-1)(㏒₂3-(х-1))=0
х=0
х-1=0
х=1
㏒₂3-х+1=0
х=㏒₂3+1
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад