Question

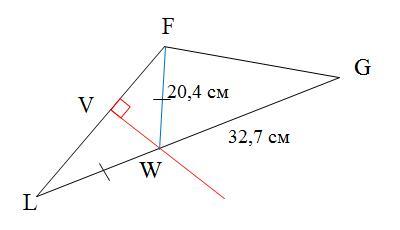
Серединный перпендикуляр, проведённый к стороне LF
треугольника LFG, пересекает сторону 
LG в точке W. Чему равна сторона LG, если FW=20,4 см, 
GW=32,7 см?

Answer 1

Ответ:

LG = 53,1 см

Пошаговое объяснение:

Дано (см. рисунок):

  ΔLFG

  FV=VL

  VW⊥LF

  FW = 20,4 см

  GW = 32,7 см  

Найти: LG.

Решение.

Рассмотрим треугольник LWF. В этом треугольнике серединный перпендикуляр VW опушен из вершины W. Тогда отрезок VW будет высотой треугольника LWF к стороне  LF.

По условию серединный перпендикуляр VW и FV=VL, откуда следует, что высота VW является и медианой. Отсюда следует, что треугольник LWF равнобедренный и:

LW=FW=20,4 см.

Остаётся найти сторону LG:

LG=LW+WG= 20,4+32,7 = 53,1 см.

#SPJ1