Ответы
Ответ дал:
1
Ответ:
126°
Решение:
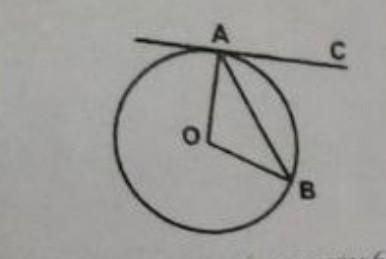
1) По условию, СА - касательная к окружности, следовательно CA⊥OA (т.к. касательная к окружности перпендикулярна радиусу окружности, проведенному к точке касания).
2) CA⊥OA, значит ∠САО=90°
3) По условию, ∠ВАС=63°
∠САО = ∠ВАС+∠ВАО, значит ∠ВАО = ∠САО-∠ВАС = 90°-63°=27°
4) ОА=ОВ как радиусы окружности, значит ΔАОВ- равнобедренный, следовательно ∠ВАО=∠АВО = 27° как углы при основании равнобедренного треугольника
5) Сумма углов треугольника равна 180° (теорема о сумме углов треугольника), значит
∠АОВ=180°-2*∠ВАО = 180° - 2*27° = 180°-54° = 126°
odilnaz051:
спасибо!!!!!!!!
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад