Ответы
Ответ дал:
0
Решение.
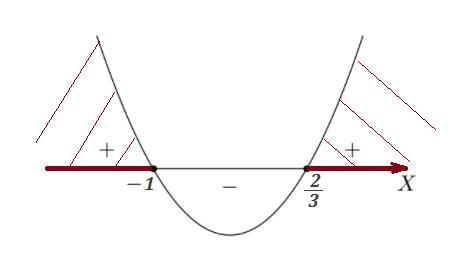
Найдём сначала нули квадратичной функции.
Так как старший коэффициент а=3>0 , то ветви параболы направлены вверх . Схематически нарисуем параболу и определим, при каких значениях х её график лежит выше оси ОХ . В этих промежутках поставлены знаки плюс .
Ответ: .
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад