Ответы
Ответ дал:
2
Решение.
Умножим первое уравнение на 12, а второе - на 6, чтобы освободиться от знаменателей .
Вычтем из первого уравнения второе .
Ответ:
Ответ дал:
1
Ответ:
на фото
Объяснение:
Приложения:
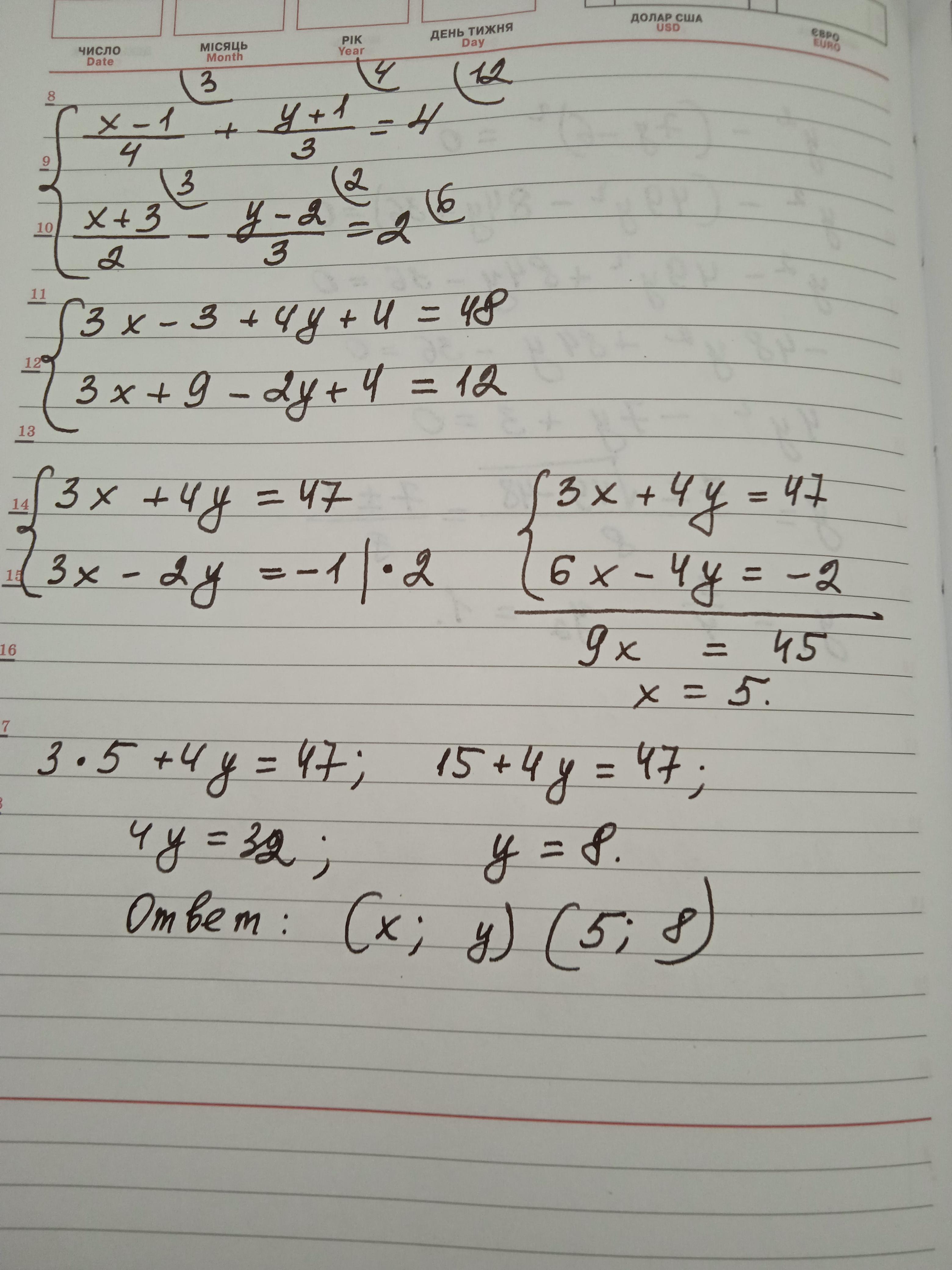
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
