Ответы
Ответ дал:
1
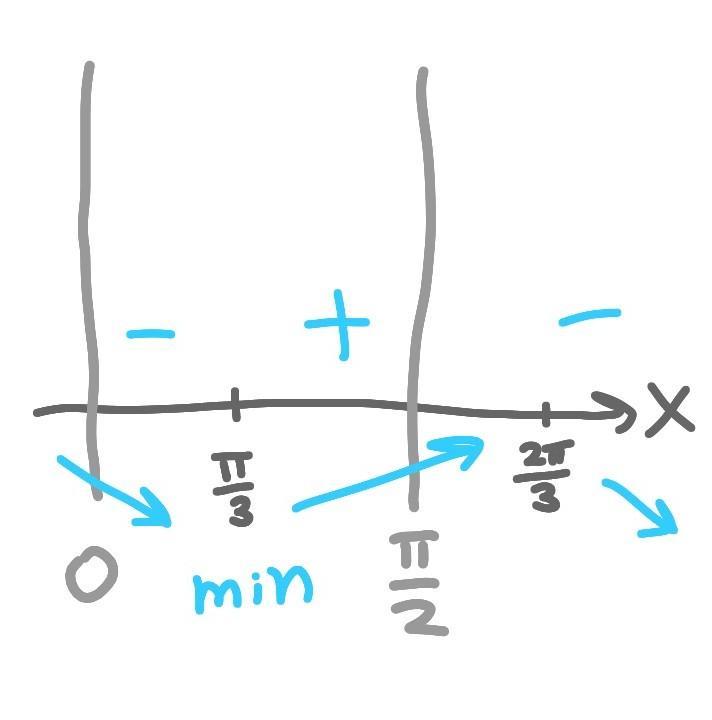
Продолжение не прикреплённом изображении.
Получим, что точка минимума функции на отрезке [0; π/2] — π/3.
Ответ: –9.
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
9 лет назад