Помогите Пожалуйста!!!!!
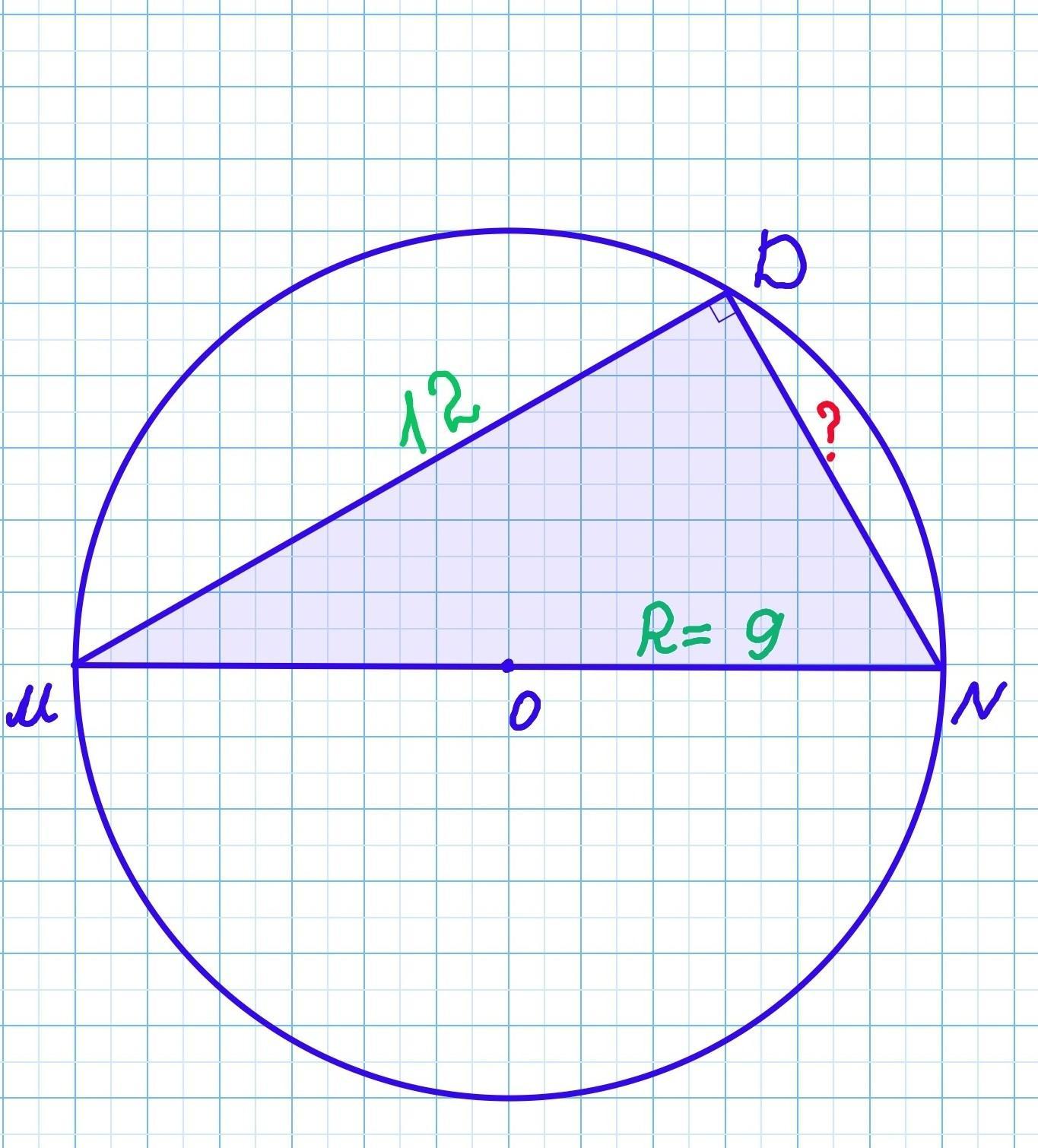
В окружности проведены диаметр MN и хорда MD. МD = 12, а радиус окружности равен 9 см. Найди длину хорды DN
Ответы
Ответ дал:
3
Ответ:
Длина хорды DN= 6√5 см
Объяснение:
В окружности проведены диаметр MN и хорда MD. МD = 12, а радиус окружности равен 9 см.
Найди длину хорды DN.
- Вписанный угол, опирающийся на диаметр окружности, — прямой.
Так как ∠MDN опирается на диаметр MN, следовательно ∠MDN=90°.
△MDN - прямоугольный.
Диаметр MN является гипотенузой △MDN.
- Диаметр окружности равен двум радиусам.
MN=D=2•R=2•9=18 см
По теореме Пифагора найдём катет DN.
DN²=MN²-MD²=18²-12²=(18-12)(18+12)=6•30=180
DN= 6√5 см
#SPJ1
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад
ΔMDN-прямоугольный , отрезок MN=2*9=18
По Пифагору DN=√(18²-12²)=....считай