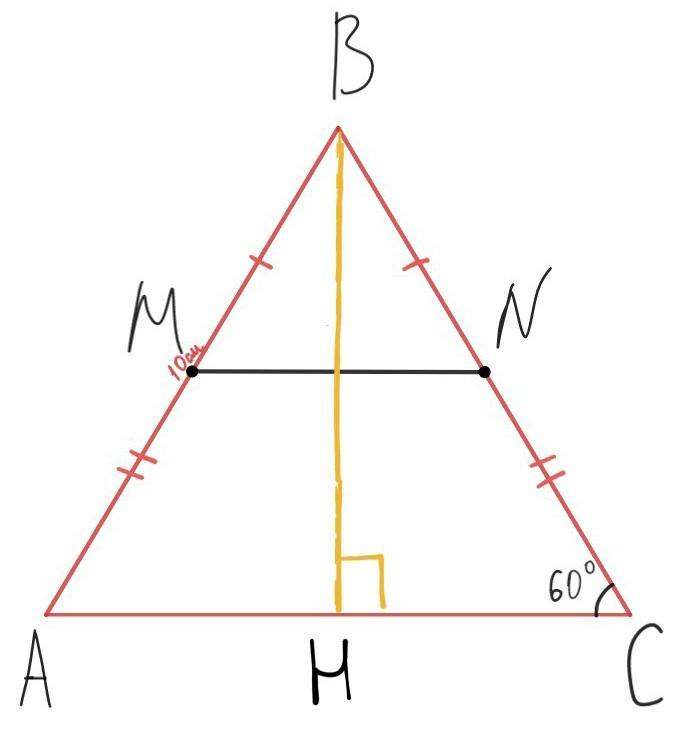
Точки M и N середины сторон AB и BC треугольника ABC. Найдите длину отрезка MN, если AB = 10 см, ∠ACB = 60°.
Ответы
Ответ дал:
3
Ответ:
Дано: ΔАВС , MN- средняя линия ΔАВС,АВ=10см , ∠АСВ=
Найти: MN
Решение:
ΔМВN~ΔABC⇒AB=BC,MB=NB.
Проведём высоту ,тогда рассм. Δ
-прямой=90°.
Половина основания большого Δ- будет являться катетом Δ
⇒
.
В Δ , ∠B=90°-60°=30°, а катет
лежит против угла 30° - значит равен половине гипотенузы
⇒
см.
Значит основание см.
Средняя линия равна половине основания :
Ответ:  см.
см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад