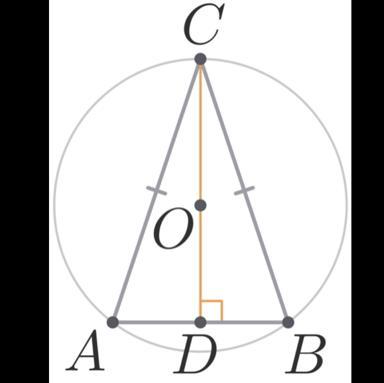
Равнобедренный треугольник ABC (AC=BC) вписан в окружность с центром O.
Известно, что AB=12, DO=8, где D — основание перпендикуляра из O на AB.
Найдите площадь треугольника ABC.
Приложения:
Ответы
Ответ дал:
0
АД= 6(АВС - р/б треугольник)
найдём АО из треугольника АОД по теореме о Пифагора и получим 10. АО является ещё и радиусом окружности, а значит равняется СО. СД= 10+ 8 = 18
S = 1/2 * CD * AB = 1/2 * 18* 12 = 108
ответ: 108
найдём АО из треугольника АОД по теореме о Пифагора и получим 10. АО является ещё и радиусом окружности, а значит равняется СО. СД= 10+ 8 = 18
S = 1/2 * CD * AB = 1/2 * 18* 12 = 108
ответ: 108
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад