Ответы
Ответ дал:
0
Ответ:
Объяснение:
Дано:
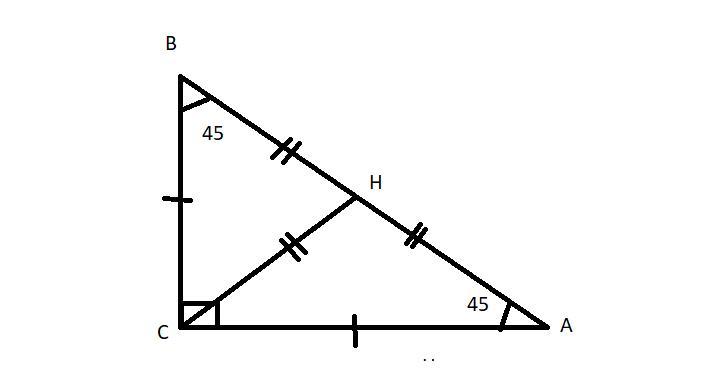
АВ=16 м
∠CBA=45°
Найти:
СА - ?
Решение:
1. ∠CAB=90°-45°=45°,
∠CBA=∠CAB, следовательно, треугольник равнобедренный,
АС=СВ
2. проведем медиану CH
она будет являться и высотой, и биссектрисой
значит, она будет делить прямой уголь пополам, на два угла по 45°
отсюда в треугольнике CHA:
треугольник равнобедренный, CH=AH=BA/2=8 м
3. угол СНА - прямой, треугольник СНА - прямоугольный
по теореме Пифагора:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад