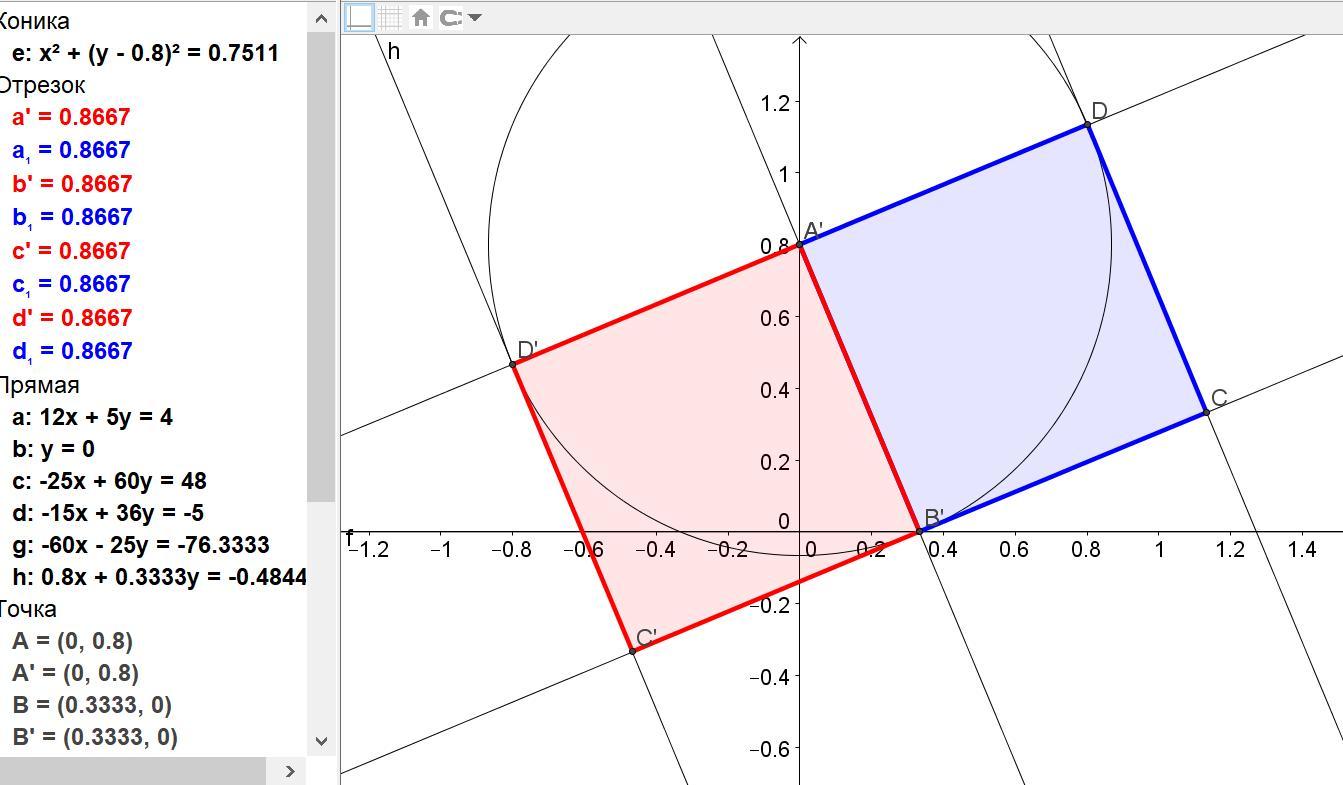
Найти уравнение прямых, на которых лежат три стороны квадрата, зная, что четвёртой стороной является отрезок прямой 12x + 5y – 4 = 0 , концы которого лежат на осях координат.
Ответы
Найти уравнение прямых, на которых лежат три стороны квадрата, зная, что четвёртой стороной является отрезок прямой 12x + 5y – 4 = 0 , концы которого лежат на осях координат.
Находим точки пересечения прямой 12x + 5y – 4 = 0 с осями Ох и Оу.
С осью Оу при х = 0: 12*0 + 5y – 4 = 0, у = 4/5, точка А(0; (4/5)).
С осью Ох при у = 0: 12x + 5*0 – 4 = 0, х = 4/12 = 1/3, точка В((1/3); 0).
Длина стороны квадрата как модуль вектора АВ равна:
Вектор АВ = ((1/3) – 0;0 –(4/5)) = ((1/3); –(4/5)).
АВ = √((1/3)² + (4/5)²) = √((1/9) + (16/25)) = √(169/225) = 13/15.
Уравнение стороны АВ: (x – 0)/(1/3)) = (y – (4/5))/(-4/5)).
Или в общем виде и с угловым коэффициентом:
-(4/5)x = (1/3)y – (4/15),
-12x = 5y – 4, 12x + 5y -4 = 0,
y = -(12/5)x + (4/15).
Уравнение прямой параллельной другой прямой y = ax + b и лежащей на заданном расстоянии (для квадрата равном АВ = L) от нее находим по формуле y=ax+c.
Коэффициент а = (-12/5), b = (4/15), значение c=b± L√(1+a²).
Подставим значения коэффициентов a и b:
c = (4/15) ± (13/15)√(1+(-12/15)²).
c1 = 1 12 144 369 19,20937271
15 225 225 15
0,266666667 1,109874868 1,3765415
-0,8432082.
Получаем 2 варианта расположения квадрата.
Уравнение стороны CD: y = -(12/5)x + 1,3765415 и
y = -(12/5)x - 0,8432082.
Составим уравнение прямой AD, проходящей через точку А(0; (4/5)) перпендикулярно прямой
АВ:12x + 5y - 4 = 0.
Прямая, проходящая через точку M1(x1; y1) и перпендикулярная прямой Ax+By+C=0, представляется уравнением
A(y-y1)-B(x-x1)=0.
Решение. Здесь A=12, B=5, точка А(0; (4/5)).Подставим значения в формулу
12(y – (4/5)) – 5(x – 0) = 0, т.е. уравнение AD: 5x –12y + (48/5) = 0 или 25x – 60y + 48 = 0.
Аналогично для прямой ВС: A=12, B=5, точка В((1/3); 0). Подставим значения в формулу:
12(y – 0) – 5(x – (1/3)) = 0, т.е. уравнение ВС: 5x –12y - (5/3) = 0 или
15x – 36y + 5 = 0.