1. Укажите соответствующий вывод для каждого неравенства. Обоснуйте свой ответ.
a) 2x ^ 2 + 8x + 20 >= 0 ; b) - x ^ 2 - 10x + 25 > 0 : c x ^ 2 + 3x + 2 <= 0 ; d) - 4x ^ 2 - 4 > 0 .
6) Решением неравенства является обьединение двух промежутков.
5) Решением неравенства является открытый промежуток.
4) Решением неравенства является закрытый промежуток.
2) Решением неравенства является вся числовая прямая.
3) Решением неравенства является одна точка.
1) Неравенство не имеет решений.
Приложения:
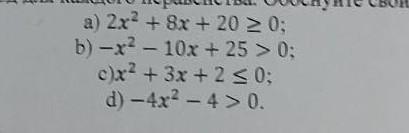
Ответы
Ответ дал:
1
Ответ: a - 2 , b - 5 , c - 4 , d - 1 .
Так как D<0 и a=1>0 , то решением является вся числовая прямая .
Решением неравенства является открытый промежуток .
Пользуясь теоремой Виета находим корни квадратного трёхчлена,
. Тогда неравенство перепишем в виде:
Решением неравенства является закрытый промежуток .
Квадрат выражения всегда неотрицателен ( больше или равен 0 ) , поэтому сумма х² и 1 будет больше 0, значит неравенство не выполняется ни при каких значениях переменной х , . Неравенство не имеет решений .
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад