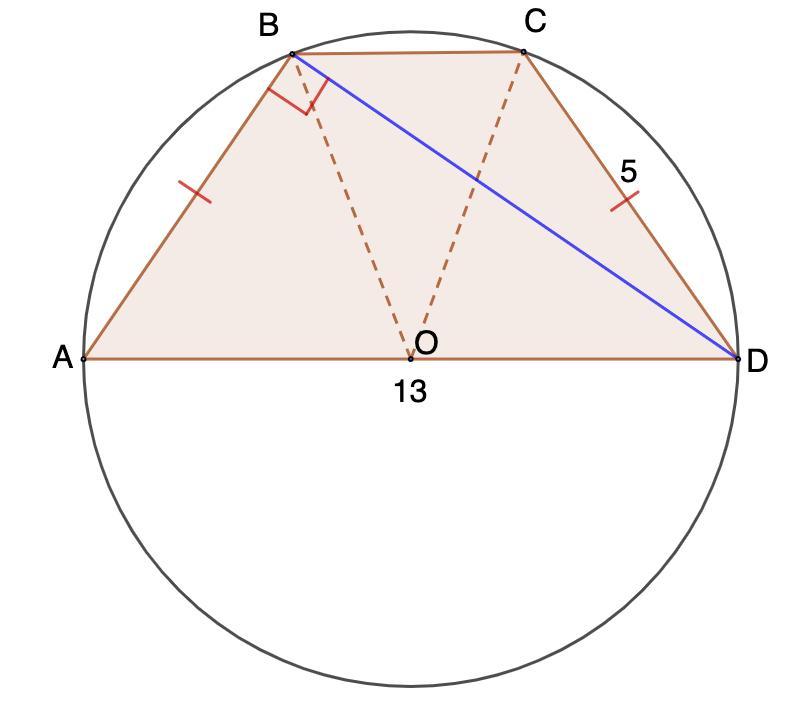
На большем основании A D трапеции A B C D как на диаметре построена окружность с центром в точке O . Оказалось, что точка O равноудалена от всех вершин данной трапеции. Найдите длину диагонали B D трапеции A B C D , если известно, что A D = 1 3 , C D = 5
Ответы
Ответ дал:
1
Ответ:
Длина диагонали BD равна 12 ед.
Объяснение:
Требуется найти длину диагонали CD.
Дано: ABCD - трапеция;
AD - диаметр Окр.О;
OA = OB = OC = OD;
AD = 13; CD = 5.
Найти: BD.
Решение:
OA = OB = OC = OD (условие)
- Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от одной точки, называемой центром окружности.
⇒ В ∈ Окр.О; С ∈ Окр.О
То есть ABCD - вписанная трапеция.
- Если трапеция вписана в окружность, то она равнобедренная.
⇒ CD = AB = 5.
Рассмотрим ΔABD.
- Если вписанный угол опирается на диаметр, то он прямой.
⇒ ΔABD - прямоугольный.
АВ = 5; AD = 13
По теореме Пифагора найдем BD:
BD² = AD² - AB² = 169 - 25 = 144
BD = √144 = 12
Длина диагонали BD равна 12 ед.
#SPJ1
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад