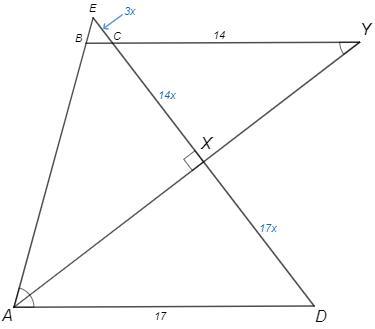
Дан четырёхугольник ABCD, в котором AD∥BC. Биссектриса угла A пересекает сторону CD в точке X, а продолжение стороны BC за точку C — в точке Y. Оказалось, что ∠AXC=90∘.
Найдите длину отрезка AB, если известно, что AD=17 и CY=14.
Ответы
Ответ дал:
4
△DXA~△CXY (стороны параллельны)
DX/CX=AD/CY =17/14
AX - биссектриса и высота, следовательно и медиана, EX=DX
EX=DX=17x, CX=14x => EC=3x
△BEC~△AED (стороны параллельны)
BC/AD=EC/ED =3/34 => BC=17*3/34 =3/2
∠BAY=∠DAY (AY -биссектриса)
∠BYA=∠DAY (накрест лежащие при BY||AD)
=> ∠BAY=∠BYA => △ABY -р/б
AB=BY =BC+CY =1,5+14 =15,5
Приложения:
cistakovd166:
А если CY 13 а AD 16?
тогда 14,5
Здравствуйте, помогите с вопросом в профиле, пожалуйста
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад