Question

Доказать методом площадей, что высота прямоугольного треугольника, проведенная до гипотенузы, равна доле произведения катетов и гипотенузы.​

Answer 1

Ответ:

Доказано, что высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна отношению произведения катетов к гипотенузе.

Объяснение:

Доказать методом площадей, что высота прямоугольного треугольника, проведенная до гипотенузы, равна доле произведения катетов и гипотенузы.​

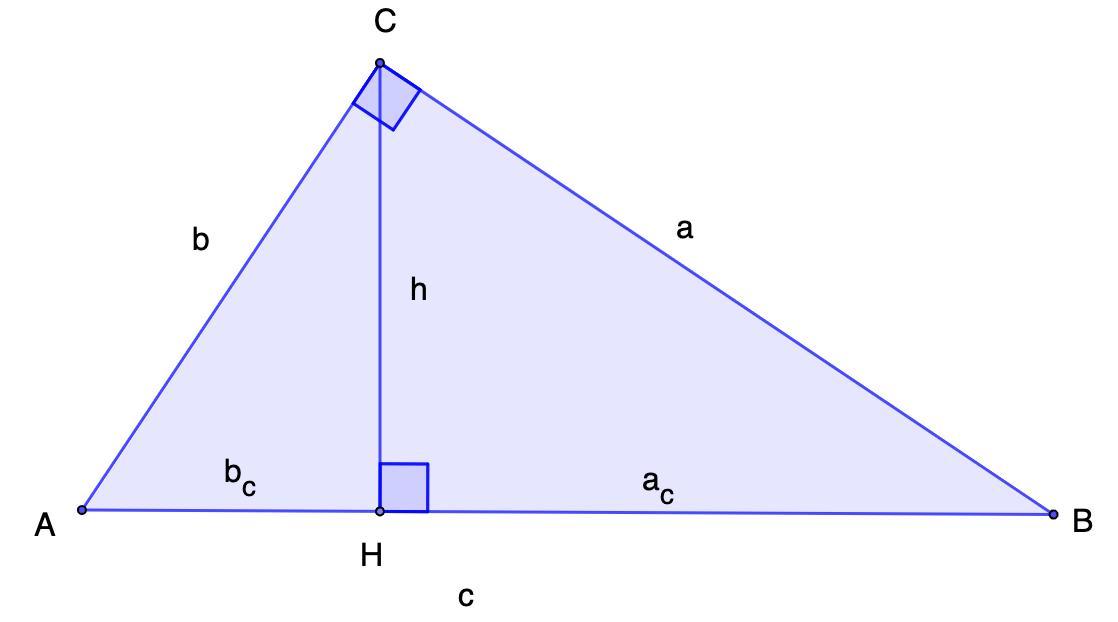
Дано: ΔАСВ - прямоугольный;

∠С = 90°;

СН - высота.

Доказать:  $\displaystyle h=\frac{ab}{c}$

Доказательство:

S (ACB) = S (ACH) + S (HCB)     (1)

• Площадь прямоугольного треугольника равна половине произведения катетов.

⇒ (см.рис)

$\displaystyle S (ACB) = \frac{1}{2}AC\cdot{CB}=\frac{1}{2}ab\\ \\ S (ACH) = \frac{1}{2}AH\cdot{HC}=\frac{1}{2}b_ch\\\\ S (HCB) = \frac{1}{2}HC\cdot{HB}=\frac{1}{2}a_ch$

В равенстве (1) заменим площади соответствующими выражениями:

$\displaystyle \frac{1}{2}ab=\frac{1}{2}b_ch+\frac{1}{2}a_ch\;\;\;\;\;|\cdot2\\ \\ ab=h(b_c+a_c)\\ \\ab=hc\\\\h=\frac{ab}{c}$

Доказано, что высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна отношению произведения катетов к гипотенузе.