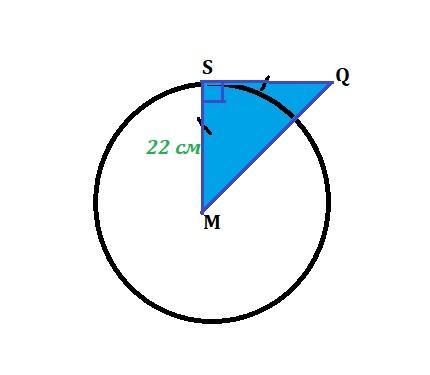
К окружности с центром M и радиусом 22 см проведена касательная SQ так, что MS = SQ . Найди значение MQ .
Ответы
Ответ дал:
1
Ответ:
MQ=22 см
Объяснение:
К окружности с центром M и радиусом 22 см проведена касательная SQ так, что MS = SQ . Найди значение MQ .
- Касательная к окружности - прямая, имеющая с окружностью только одну общую точку.
- Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Решение
MS - радиус окружности. MS = 22 см
SQ - касательная к окружности, проведенная в точку касания S.
Тогда по свойству касательной к окружности:
MS ⊥ SQ, ΔМSQ - прямоугольный, ∠S=90°.
По теореме Пифагора найдём гипотенузу MQ:
MQ²= MS² + SQ² = 22²+22²=484+484=2*484
MQ= см
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад