Question

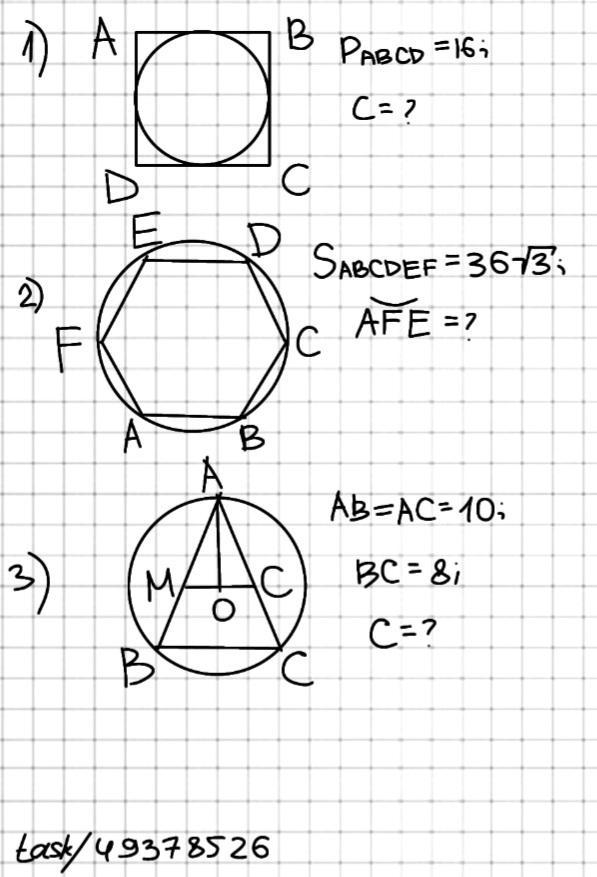
1)Вокруг окружности описан квадрат АВСD, с периметром 16 . Найдите С-длину окружности .

2)В окружность вписан правильный шестиугольник ABCDEF, с площадью 36√3.
Найдите длину АFE.

3)В окружность вписан равнобедренный треугольник АВС , АВ=АС=10 ,основание ВС=8.Найдите С-длину окружности.​

Answer 1

задание 1.

Вокруг окружности описан квадрат АВСD, с периметром 16 . Найдите С-длину окружности

__________________________________

• найдем диаметр, в данном случае это сторона квадрата, описанного около окружности: $DC=P/4=16/4=4$;
• найдем радиус: $R=DC/2=4/2=2$;
• найдем длину окружности: $C=2\pi R=2\pi *2=4\pi$

ответ: $C=4\pi$

задание 2.

В окружность вписан правильный шестиугольник ABCDEF, с площадью 36√3.Найдите длину АFE.

__________________________________

• формула нахождения площади правильного многоугольника,вписанного в окружность: $\displaystyle S=\frac{n}{2} *R^2*sin\frac{2\pi }{n}$, где $n$-число сторон многоугольника,$\pi =180^\circ$.выразим из нее радиус и вычислим его: $\displaystyle S=\frac{n}{2} *R^2*sin\frac{2\pi }{n};\\\frac{R^2n}{2} =\frac{S}{\displaystyle sin\frac{2\pi }{n} } ;\\R=\sqrt{\frac{2S}{n*sin\displaystyle \frac{2\pi }{n} } } =\sqrt{\frac{2*36\sqrt{3} }{6*sin\displaystyle\frac{360^\circ}{6} } } =\\=\sqrt{\frac{72\sqrt{3} }{6*\displaystyle \frac{\sqrt{3} }{2} } } =\sqrt{\frac{72\sqrt{3} }{3\sqrt{3} } } =\sqrt{24};$
• представим окружность,как три дуги,равные между собой. тогда одну из них можно найти,поделив длину окружности на три: $\displaystyle C=2\pi R;\\C=2\sqrt{24} \pi ;\\\breve{AFE}=\frac{2\pi \sqrt{24} }{3} =\frac{4\pi \sqrt{6} }{3}$

ответ: $\displaystyle \breve{AFE}=\frac{4\pi \sqrt{6} }{3}$

задание 3.

В окружность вписан равнобедренный треугольник АВС , АВ=АС=10 ,основание ВС=8.Найдите С-длину окружности.

__________________________________

• выделим среднюю линию $\Delta ABC$-$MC$. она параллельна $BC$ и равна одной второй ее части: $MC=BC/2=8/2=4$;
• проведем высоту у $\Delta AMC$-$AO$, она будет численно равна радиусу данной окружности. найдем его по теореме Пифагора: $MA^2=AO^2+MO^2;\\AO^2=MA^2-MO^2;\\AO^2=25-4=21;\\AO=R=\sqrt{21}$
• найдем длину окружности: $C=2\pi R=2\pi *\sqrt{21} =2\sqrt{21} \pi$

ответ: $C=2\sqrt{21} \pi$