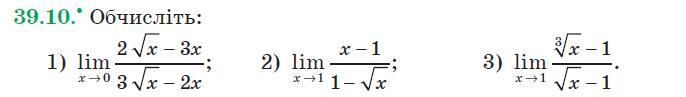Ответы
Ответ дал:
1
Ответ:
Пределы:
1)
2)
3)
Примечание:
если
----------------------------------------------------------------------------------------------------------
Следствие из предела произведения:
Объяснение:
39.10
1)
2)
3)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад