Задание 1.

Задана функция y = −x2 + 4x − 7.

Найдите:

а) область определения данной функции (6 баллов);

б) область значений данной функции (10 баллов).

Задание 2 (16 баллов).

Задана функция y = −4x2 + 8x + c. Определите значение c, при котором наибольшее значение функции равно 7.

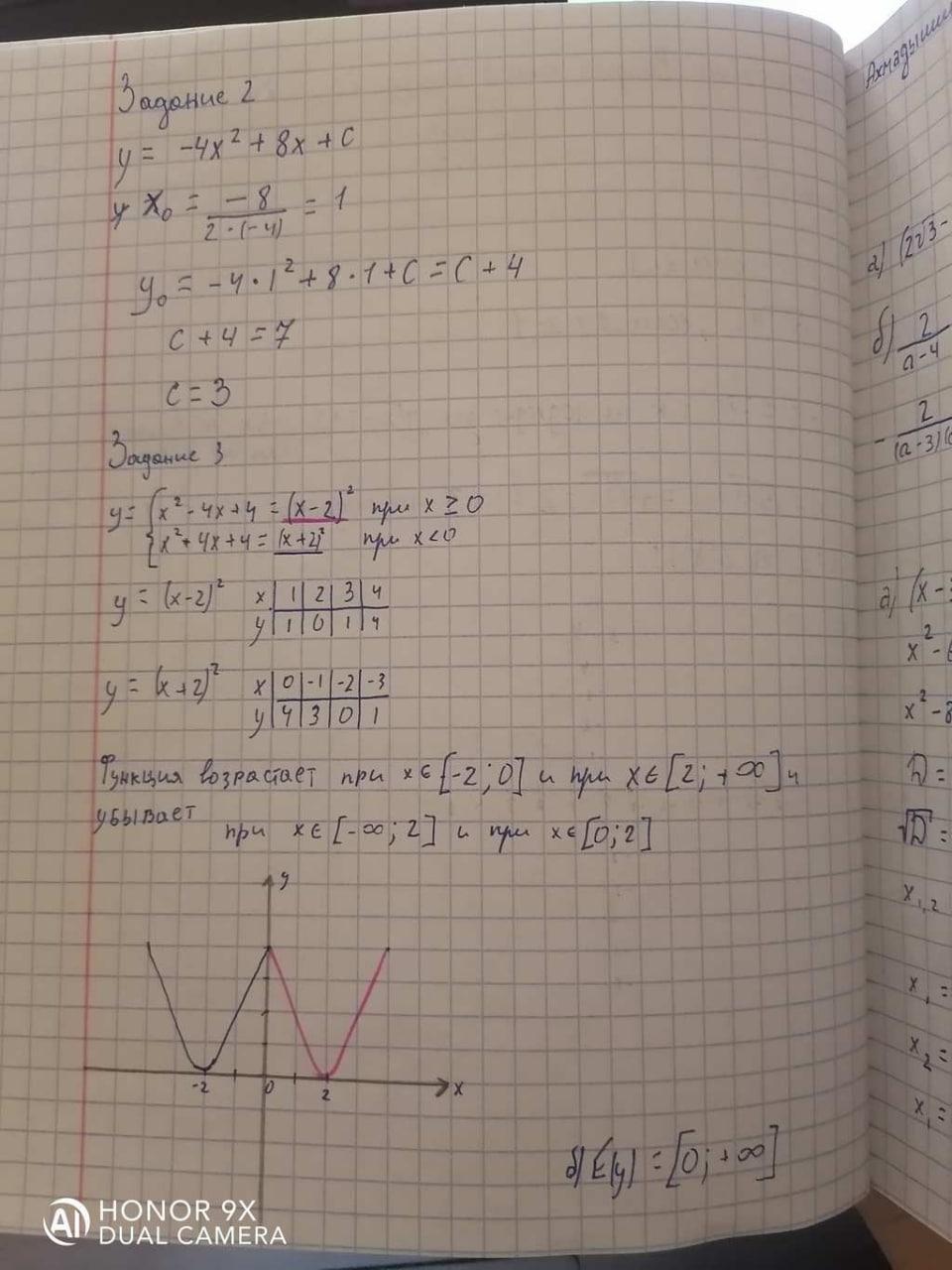
Задание 3.

Задана функция y = x2 − 4|x| + 4.

а) Постройте график данной функции (22 балла).

б) По графику функции определите:

область значений функции (6 баллов);
промежутки возрастания и убывания функции (8 баллов).

Ответы

Ответ дал: Unicorn00023

Ответ:

Всё в закрепе (ещё не проверили)

Пошаговое объяснение:

Приложения:

evgunk: у=ах²+bх+cпервый коэффициент а=-1- указывает на то, что график функции - парабола, направлена ветвями вниз, поэтому наименьшего значения функция не имеет, а наибольшее в вершине, координаты которой находят по формуле x=-b/2a=-4/(-2)=2; у(2)=-4+4*2-7=-3

а) область определения D(у)=(-∞;+∞),

б) область значений Е(у)=(-∞;-3]

evgunk: у=ах²+bх+c, первый коэффициент а=-1- указывает на то, что график функции - парабола, направлена ветвями вниз, поэтому наименьшего значения функция не имеет, а наибольшее в вершине, координаты которой находят по формуле x=-b/2a=-4/(-2)=2; у(2)=-4+4*2-7=-3

а) область определения D(у)=(-∞;+∞),

б) область значений Е(у)=(-∞;-3]

evgunk: просто в 1 задании я не очень понял как ты определил(а)

evgunk: -2 в квадрате будет +4, 4 + 8(4*2) = 12, 12 - 7 = 5

evgunk: там где у=(х+2)^2, когда х равен -1, у = 1, а не 3

HelpxMaryam: привет! у тебя есть информатика 34 неделя? если да, то ответь пожалуйста на мой вопрос.

Вас заинтересует

Беларуская мова

1 год назад

Помогите пожалуйста :Просклонять дроби :5/8 и 7/9

Русский язык

1 год назад

Помогите сделать морфологический разбор слов(виден,песок,сосновый) Срочно!!!

Русский язык