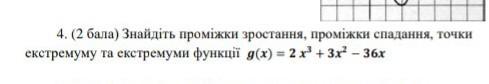Ответы
найти промежутки убывания и возрастания. точки экстремума и экстремумы функции g(x)=2x³+3x²-36x .
РЕШЕНИЕ
область определения функции х∈(-∞;+∞)
производная g'(x)=(2x³+3x²-36x)'=6х²+6х-36=6*(х²+х-6)
критические точки найдем из условия 6*(х²+х-6)=0
6≠0; х²+х-6=0; по теореме, обратной теореме Виета х=-3, х=2
решим неравенство g'(x)≤0 методом интервалов. т.е. (х+3)*( х-2)≤0,
___-3_____2_______
+ - +
на промежутках (-∞;-3] и [2;+∞) функция возрастает. т.к. там производная больше нуля. на промежутке [-3;2] убывает.
точки экстремума: х= -3- точка максимума, т.к. при переходе через нее производная меняет знак с плюса на минус. максимум равен
у(-3)=2*(-3)³+3*(-3)²-36*(-3)=-54+27-108=-135
х= 2- точка минимума, т.к. при переходе через нее производная меняет знак с минуса на плюс. минимум равен
у(2)=2*2³+3*2²-36*2=16+12-72=-44