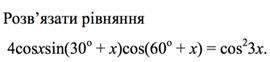Ответы
Ответ дал:
0
Ответ:
Объяснение:
Решить тригонометрическое уравнение:
Представим угол (30° + х) в виде (90° - (60° - х)) и воспользуемся формулой приведения:
Применим формулу преобразования произведения в сумму (1):
Применим формулу (1) еще раз:
1)
2)
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад