Помогите пожалуйста с алгеброй!!!!! Очень надо!!!!! Номер 27.6 (1, 3)
Найдите общее решение дифференциального уравнения:
11 КЛАСС!!!!!! КТО ЗНАЕТ ОТВЕТ!!!!!
Приложения:
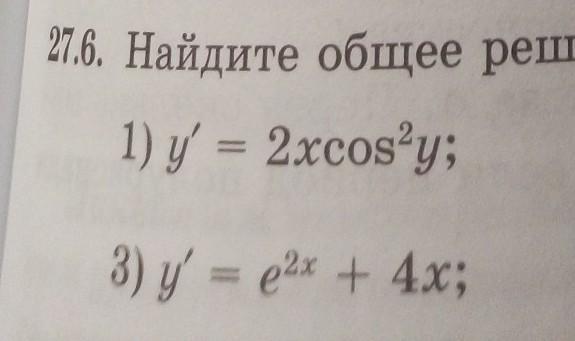
Ответы
Ответ дал:
1
Объяснение:
1.
y'=2xcos²y
∫ =∫
⇒sin(y)-x²cos(y)= C cos (y), y=
2.
y'=+4x
+4x
dy=(+4x)dx
∫1dy=∫+4xdx
y=, C= const
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад