Пожалуйста помогите. Это очень срочно. Внутри параллелограмма ABCD выбрали произвольную точку Е. Докажите, что сумма площадей треугольников AEB и CED равна половине площади параллелограмма.
Ответы
Ответ дал:
1
Объяснение:
Решение.
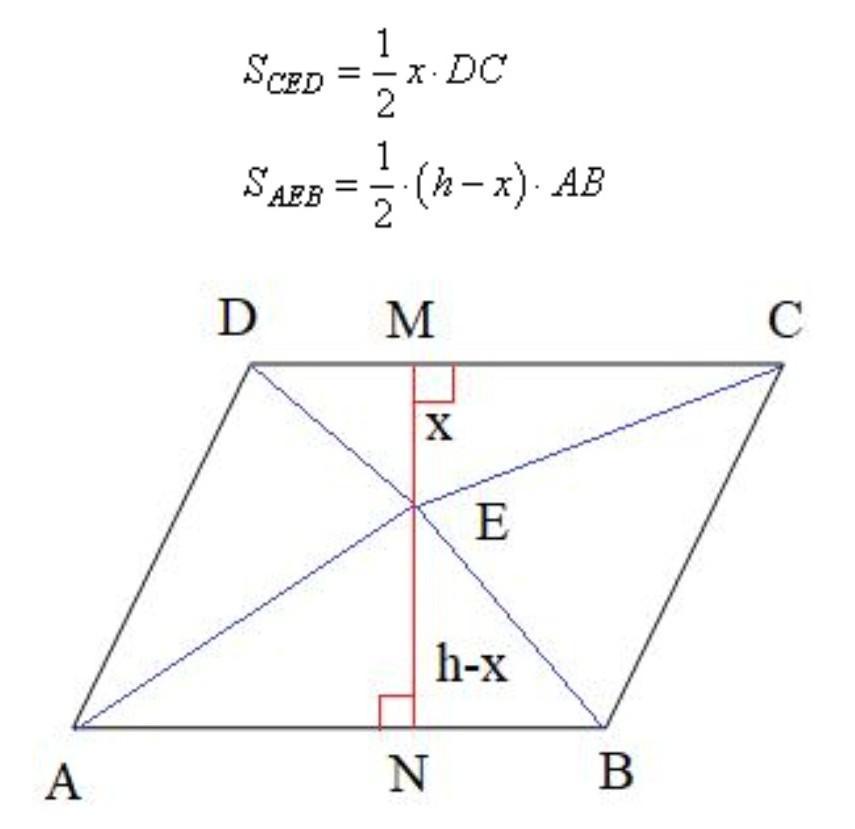
Проведем в параллелограмме ABCD высоту MN, равную h, и проходящую через точку E. Пусть расстояние ME=x, тогда NE=h-x. Площадь параллелограмма можно вычислить как
(1 картина)
а площади треугольников как
(2 картина)
Так как в параллелограмме противоположные стороны равны, то AB=CD и сумма площадей треугольников равна
(3 картина)
что в точности равно половине площади параллелограмма ABCD. Утверждение доказано.
Приложения:
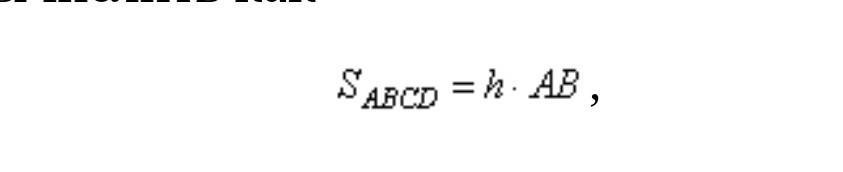
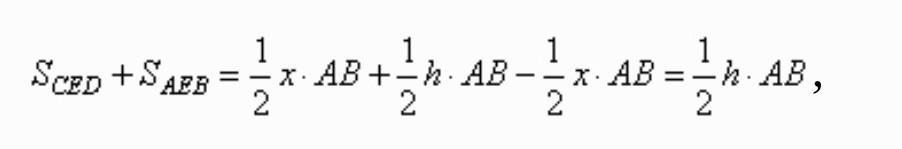
alimak0103:
огромнейшее спасибо
))
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад