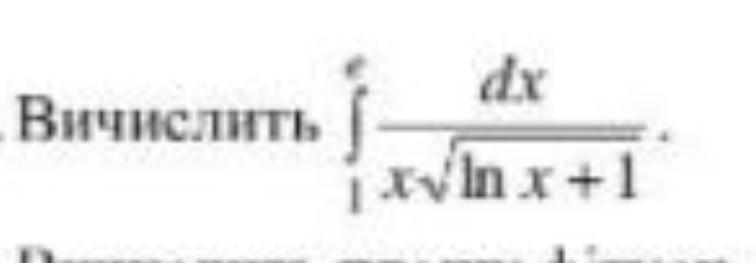Ответы
Ответ дал:
1
Ответ: 2*(√2-1).
Пошаговое объяснение:
Обозначим искомый интеграл через I. По формуле Ньютона-Лейбница, I=F(e)-F(1), где F(x)=∫dx/{x*√[ln(x)+1]}. Так как dx/x=d[ln(x)], то F(x)=∫d[ln(x)]/{√[ln(x)+1]}. Положим ln(x)=u, тогда данный интеграл примет вид F(u)=∫du/√(u+1)=∫d(u+1)/√(u+1)=2*√(u+1)+C. Отсюда F(x)=2*√[ln(x)+1]+C. Тогда I=2*√[ln(e)+1]+C-2*√[ln(1)+1]-C=2*√2-2=2*(√2-1).
alexandrovkaterina:
Спасибо Вам большое , а вы не могли бы написать это на бумаге или как то ещё, а то я не очень понимаю как его записать
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад