Question

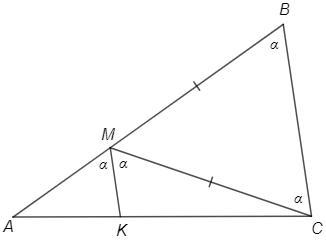
На стороне AB треугольника ABC отметили точку M так, что BM = CM. Отрезок MK — биссектриса треугольника AMC. Докажите, что MK || BС.
С рисунком пожалуйста!!!35 баллов

Answer 1

В равнобедренном треугольнике углы при основании равны.

△BMC - р/б => ∠MBC=∠MCB =a

Внешний угол треугольника равен сумме внутренних, не смежных с ним.

∠AMC =∠MBC+∠MCB =2a (∠AMC - внешний угол △BMC)

Биссектриса делит угол пополам.

∠AMK =∠AMC/2 =a

=> ∠AMK =a =∠MBC

Если соответственные углы при двух прямых и секущей равны, то две прямые параллельны.

∠AMK =∠MBC (соответственные при MK и BC) => MK||BC