СРОЧНО ДАЮ 30 БАЛОВ
Знайдіть найменше та найбільше значення функції на заданому проміжку:
1) f(x) = x^4 -8x+5 [-3;2]
2)f(x) = 2х^3 +9х^2-60x-7 [-1 ; 3]
Ответы
Ответ дал:
0
Ответ:
1) f(x) = -8x+5 [-3;2]
f'(x)=( -8x+5)'=4х³-16
f'(x)=0
4х³-16=0
4х(х²-4)=0
х1=0
х²-4=0
х2,3=±2
f(0)=-8*0²+5=5
f(-3)=-8*(-3)²+5=14 - найбільше значення функції
f(-2)=-8*(-2)²+5=-11 - найменше значення функції
f(2)=-8*2²+5=-11
f(x)max[-3;2]=f(-3)=14
f(x)min[-3;2]=f(-2)=-11
2)f(x) = 2х³ +9х²-60x-7 [-1 ; 3]
f'(x) = 6x² + 18x - 60
6x² + 18x - 60 = 0 /:6
x² + 3x - 10 = 0
D = 9 + 40 = 49
x1 = - 5
x2 = 2
f(0)=2х³ +9х²-60x-7=2*0³+9*0²-60*0-7=-7
f(-1) = 2*(-1)³+9*(-1)²-60*(-1)-7=-2+9+60-7=60 - найбільше значення функції
f(3) = 2*3³+9*3²-60*3-7=54+81-180-7=-52 - найменше значення функції
f(x)max[-3;2]=f(-1)=60
f(x)min[-3;2]=f(3)=-52
Ответ дал:
1
дивіться фото.....................
Приложения:
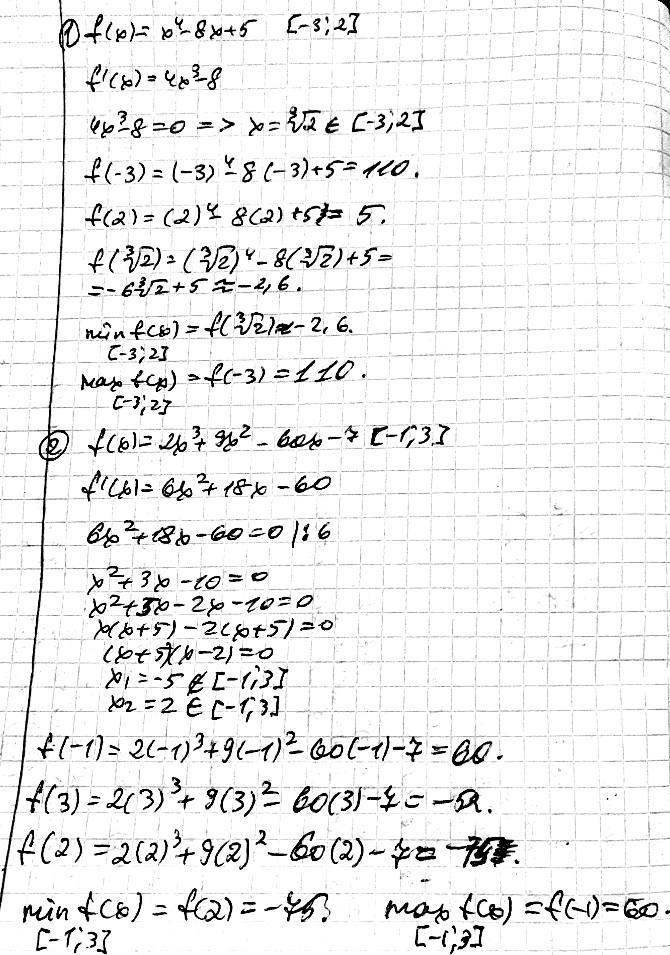
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад