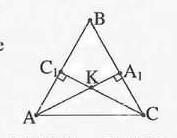
В треугольнике ABC высоты AA1 и CC1 пересекаются в точке K. Найдите угол AKC, если угол BCA = 55° и угол BAC = 65°.
Приложения:
FaerVator:
ответ какой должен быть?
Варианты ответа:
А) 140°
B) 120°
C) 115°
D) 125°
E) 110°
Ответы
Ответ дал:
1
Ответ:
120°
Объяснение:
Внешний угол треугольника равен сумме внутренних, не смежных с ним.
B' =A+C =65°+55° =120° (внешний угол ABC при вершине B)
BC1KA1 - вписанный (т.к. противоположные углы прямые)
Внешний угол вписанного четырехугольника равен противолежащему внутреннему.
K =B' =120°
B' - внешний угол четырехугольника при вершине B. A1KC1 - противолежащий ему внутренний угол. AKC =A1KC1 =B'
Ясно.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад