ПОЖАЛУЙСТА ОЧЕНЬ НУЖНО ОТДАЮ ПОСЛЕДНИЕ БАЛЛЫ!!
В прямоугольном треугольнике ABC угол C равен 90 градусов проведена высота CH угол АCH равен 30° Найдите длину CH если CB равен 18 см
Ответы
Ответ дал:
2
Решение в приложении
Объяснение:
Высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу
Приложения:
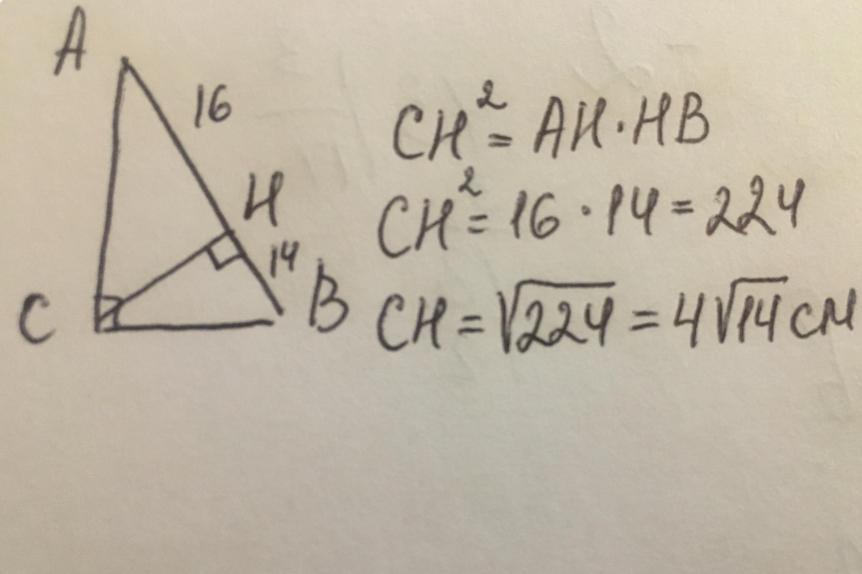
gnatynskiy:
ответ какой?
лол это не то
1 звезда от силы за решение
Ответ дал:
5
Ответ:
СН=9
Объяснение:
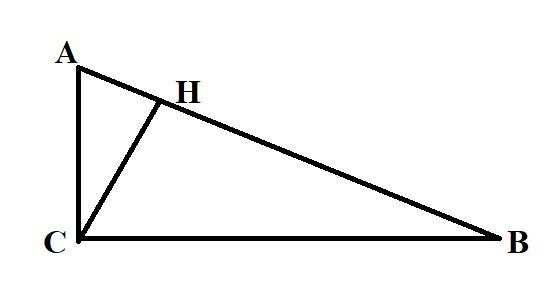
В прямоугольном треугольнике ΔАСН угол ∠АСН=30° ⇒ ∠А=60°.
В прямоугольном ΔАВС угол ∠А=60° ⇒ ∠В=30°.
Рассмотрим ΔВСН. СВ=18 - это гипотенуза, СН - катет, лежащий против угла ∠В=30°.
Поскольку в прямоугольном треугольнике против угла в 30° лежит катет, длина которого в два раза меньше длины гипотенузы, то
СН=СВ/2=18/2=9
Приложения:
Вас заинтересует
2 года назад
8 лет назад
9 лет назад
9 лет назад