Question

Срочно!! Даю 50 балів
Завдання:
y=(2x):(x^2+x+1)
Умова в фото

Answer 1

$y=\frac{2x}{x^2+x+1}$

1. Область визначення

x є (-∞;+∞).

2. Парність, непарність

Функція не є тригонометричною - періодичність не знаходимо.

$y(-x)=\frac{2(-x)}{(-x)^2+(-x)+1} =-\frac{2x}{x^2-x+1} \\y(-x) \neq y(x)\\y(-x) \neq -y(x)$

Функція ні парна, ні непарна.

3. Точки перетину з осями координат

Знайдемо точки перетину з віссю ординат Oy, тому прирівнюємо x до 0:

$y=\frac{2*0}{0^2+0+1}=2.$

Таким чином, точка перетину з віссю Oy має координати (0; 2).

Знайдемо точки перетину з віссю абсцис Ox, для цього прирівнюємо y до 0:

$\frac{2x}{x^2+x+1}=0\\2x=0\\x=0$

Таким чином, точка перетину з віссю Ox має координати (0; 0).

4. Похідна функції та критичні точки

$y=\frac{2x}{x^2+x+1}\\y'=(\frac{2x}{x^2+x+1})'=\frac{(2x)'*(x^2+x+1)-2x*(x^2+x+1)'}{(x^2+x+1)^2} =\frac{2(x^2+x+1)-2x*(2x+1)}{(x^2+x+1)^2} =\frac{-2x^2+2}{(x^2+x+1)^2} .$

$\frac{-2x^2+2}{(x^2+x+1)^2} =0\\-2x^2+2=0\\-2x^2=-2\\x^2=1\\x_{1} =1\\x_{2} =-1.$

Отже, критичні точки: 1, -1.

5. Проміжки зростання, спадання та екстремуми функції

        _                       +                     _  

--------------------(-1)------------(1)-----------------------

       f'(x)<0            f'(x)>0            f'(x)<0

    спадає             зростає         спадає

В точці x = -1 похідна функції змінює знак з (-) на (+). Отже, точка x = -1 – точка мінімуму. В точці x = 1 похідна функції змінює знак з (+) на (-). Отже, точка x = 1 – точка максимуму. Точка мінімуму і максимуму і є екстремумами функції.

6. Поведінка функції на кінцях проміжків області визн.

Оскільки у нас область визначення x є (-∞;+∞), дослідження неможливе.

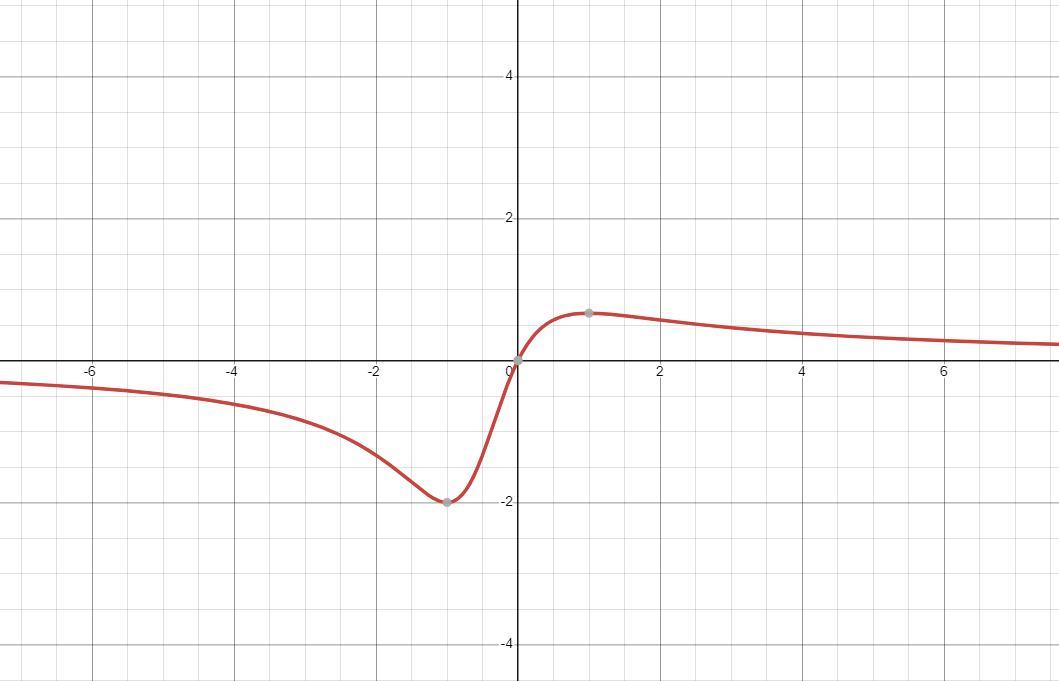
7.  *фото*