Question

прошу помогите :(((
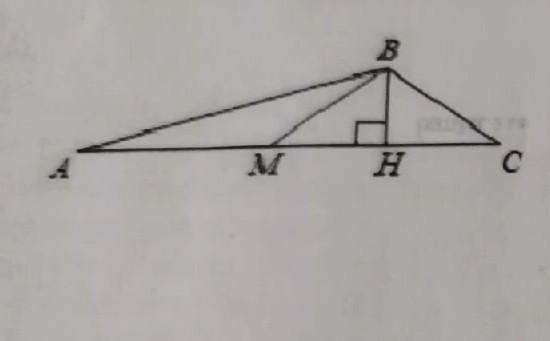
в треугольнике ABC BM - медиана и BH- высота. Известно, что AC=180 см, HC=45 см и угол AMB=120°. Найдите угол BCM и сторону BC. Ответ дайте в градусах.
подробно пожалуйста!!!!​

Answer 1

Ответ:

АС=180, ВМ-медиана, следовательно АМ=МС=180:2=90

МС-НС=МН, 90-45=45

Угол ВМН равен 180-120=60 градусов(т.к. углы АМВ и ВМН смежные)

Рассмотрим треугольник ВМН:

1)Он прямоугольный( Т.к. ВН - высота)

2)Угол ВМН равен 60, следовательно угол МВН равен 90-60=30

По теореме, катет лежащий против угла 30 градусов равен $\frac{1}{2}$ гипотенузе, поэтому МВ равно 90

Треугольник МВС:

1) МС=90(т.к. МВ медиана)

2)МВ=90(нашли)

следовательно треугольник равнобедренный

угол ВМС равен 60, следовательно угол МВС+угол ВСМ=180-69

Следовательно все углы в треугольник МВС равны по 60 и треугольник равносторонний, и ВС равно 90

Ответ: 90см, 60 градусов