Question

За даними малюнку доведіть, що ∆ABD = ∆ACD.

Answer 1

Ответ:

Треугольник ∆ABD = ∆ACD по второму признаку равенства треугольников (детальнее смотрите доказательство)

Объяснение:

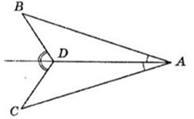
Запишем дано для данной задачи согласно рисунку:

Дано: ∠BAD = ∠DAC, угол смежный с углом ∠BDA = угол смежный с углом ∠CDA

Доказать: ∆ABD = ∆ACD

Доказательство:

Так как углы смежные с углами ∠BDA и ∠CDA равны согласно условию (рисунку), то и сами углы тоже равны, то есть ∠BDA = ∠CDA.

Треугольник ∆ABD = ∆ACD по второму признаку равенства треугольников, так как:

По условию:

• ∠BAD = ∠DAC

Доказано:

• ∠BDA = ∠CDA

Сторона AD - общая.

#SPJ1