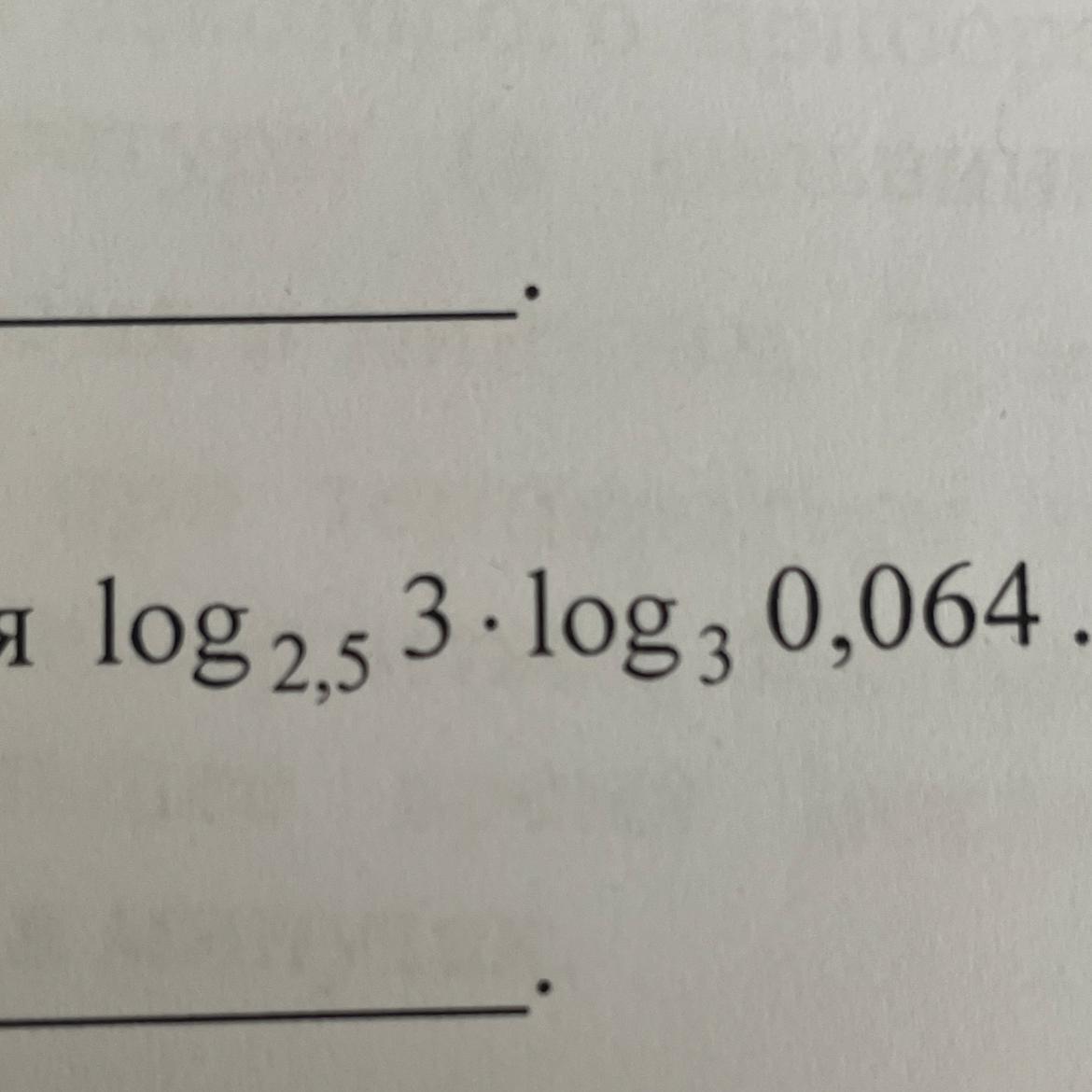Ответы
Ответ дал:
1
Ответ:
Значение выражения
Объяснение:
Найти значение выражения
.
Воспользуемся свойствами логарифмов:
Воспользуемся еще одним свойством:
#SPJ1
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад